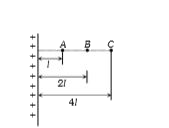
At a distance l from a uniformly charged long wire, a charged particle is thrown radially outward with a velocity u in the direction perpendicular to the wire. When the particle reaches a distance 2l from the wire its speed is found to be √2u. The magnitude of the velocity, when it is a distance 4l away from the wire, is (ignore gravity)
√3u
2 u
2√2u
4 u
The correct Answer is:A
Energy conservation at A and B
qVA+12mu2=qVB+12×2mu2⇒q[VA−VB]=12mu2
q×λ2πε0ln2=12mu2
Energy conservation at A and C
q[VA−VC]+12mu2=12mv2=12mv2
⇒qλ2πε0ln4+12mu2=12mv2
2qλ2πε0ln2+12mu2=12mv2
⇒32u2=12v2⇒v=√3u
Topper's Solved these Questions
- ELECTROSTATICSBOOK - ERRORLESSCHAPTER - ELECTROSTATICSEXERCISE - NCERT BASED QUESTIONS (Electric Field and Potential)
129 Videos
- ELECTROSTATICSBOOK - ERRORLESSCHAPTER - ELECTROSTATICSEXERCISE - NCERT BASED QUESTIONS (Electric Dipole)
21 Videos
- ELECTRONICSBOOK - ERRORLESSCHAPTER - ELECTRONICSEXERCISE - Assertion & Reason
26 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - ERRORLESSCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - ASSERTION & REASON
18 Videos
Similar Questions
A rod of length l is kept parallel to a long wire carrying constant current i . It is moving away from the wire with a velocity v.F∈dtheemf∈duced∈thewirewhenitsdistance∈thewirewhenitsdistanceomthelongwireisx.
View SolutionA rod of length l is placed perpendicular to a long wire carrying current i. The rod is moved parallel to the wire with a velocity v. Find the emf induced in the rod, if its nearest end is at a distance a from the wire.

View Solution
Knowledge Check
For a long wire of charge density γ,, field at a distance r from the wire is
Aγ2πε0rnBγ4πε0rnC0DkqεeA charge particle q is released at a distance R∘ from the infinite long wire of linear charge density λ. Then velocity will be proportional to (At distance R from the wire)
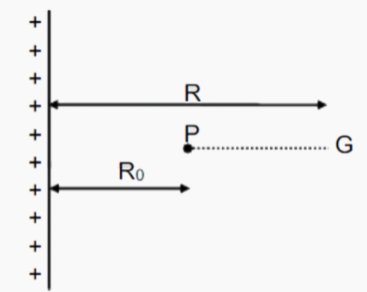 AR3BeR/R0CR2D[n(RR0)]−1/2
AR3BeR/R0CR2D[n(RR0)]−1/2Each of two long parallel wires carries a constant current i along the same direction . The wires are separated by a distance 2I. The magnitude of resultant magnetic induction in the symmetric plane of this system located between the wires at a distance R from each wire will be
Aμ0iπRBzeroCμ0iπ√R2−l2Dμ0iπR√1−l2R2
A rod of length l is placed perpendicular to a long wire carrying current i. The rod is moved parallel to the wire with a velocity v. Find the emf induced in the rod, if its nearest end is at a distance ‘a’ from the wire.
View SolutionA very long wire carrying a current I=5.0A A is bent at right angles. Find the magnetic induction at a point lying on a perpendicular to the wire, drawn through the point of hending at a distance l=35cm from it.
View SolutionA very long wire carrying a current I=5.0A A is bent at right angles. Find the magnetic induction at a point lying on a perpendicular to the wire, drawn through the point of hending at a distance l=35cm from it.
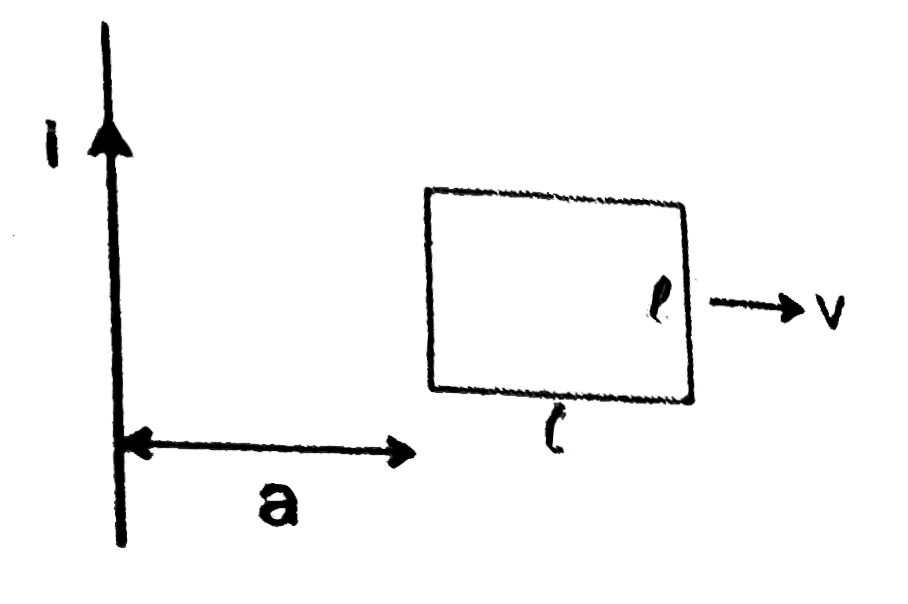
View SolutionA square meallic loop of side l is placed near a fixed long wire carrying a current i (figure). The loop is moved towards right perpendicular to the wire with a speed v in the plane containing the wire and the loop. The emf induced in the loop when the rear end of the loop is at a distance a=2l from the wire is μ0ivxπ. Find out value of x .
View SolutionA long wire carries a current of 5A. An electron at a distance of 50 cm from this wire is moving with a speed of 107 m/s What is the force acting on the electron, when it moves directly towards the wire ?
View Solution
