A particle of mass m and charge +q is located midway between two fixed charged particles each having a charge +q and at a distance 2L apart. Assuming that the middle charge moves along the line joining the fixed charges, calculate the frequency of oscillation when it is displaced slightly.
2√π3Mε0dQq
2√π2Mε0d3Qq
2√π3Mε0d3Qq
2√π3Mε0Qqd3
The correct Answer is:C
Force on displacement x
F=−K[Qq(d−x)2−Qq(d+x)2]
⇒F=−4KQqxd2 if d>>x
( -ve sign is due to restoring force)
For SHM a=−ω2x ....(i)
a=FM=−4KQqxMd3 ...(ii)
By (i) & (ii)
ω2=4KQqMd3⇒ω=√4Qq4πε0d3M
T=2π√πε0d3MQq=2√π3Md3ε0Qq
Topper's Solved these Questions
- ELECTROSTATICSBOOK - ERRORLESSCHAPTER - ELECTROSTATICSEXERCISE - NCERT BASED QUESTIONS (Electric Field and Potential)
129 Videos
- ELECTROSTATICSBOOK - ERRORLESSCHAPTER - ELECTROSTATICSEXERCISE - NCERT BASED QUESTIONS (Electric Dipole)
21 Videos
- ELECTRONICSBOOK - ERRORLESSCHAPTER - ELECTRONICSEXERCISE - Assertion & Reason
26 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - ERRORLESSCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - ASSERTION & REASON
18 Videos
Similar Questions
A particle of mass m and charge q is located midway between two fixed charged particles each having a charge q and a distance 2l apart. Prove that the motion of the particle will be SHM if it is displaced slightly along the line connecting them and released. Also find its time period.
View SolutionA charged particle of mass m having charge q remains in equilibrium at height d above a fixed charge Q. Now the charged particle is slightly displaced along the line joining the charges, show that it will executes S.H.M. and find the time period of oscillation.
View Solution
Knowledge Check
A particle of mass m and charge q is located midway between two fixed charged particles each having a charge q and at a distance 2L apart so that distance of this charge from each charge located at end is L. Assuming that the middle charge moves along the line joining the fixed charges. The frequency of oscillation when it is displaced slightly is
Aqπ√mπε0L3Bq4π(mπε0L3)C2qπ√mπε0L3Dq2π√mπε0L3Two positively charged particles each having charge Q and are d distance apart. A third charge is introduced in midway on the line joining the two charges. Find the nature and magnitude of third charge so that the system is in equilibrium.
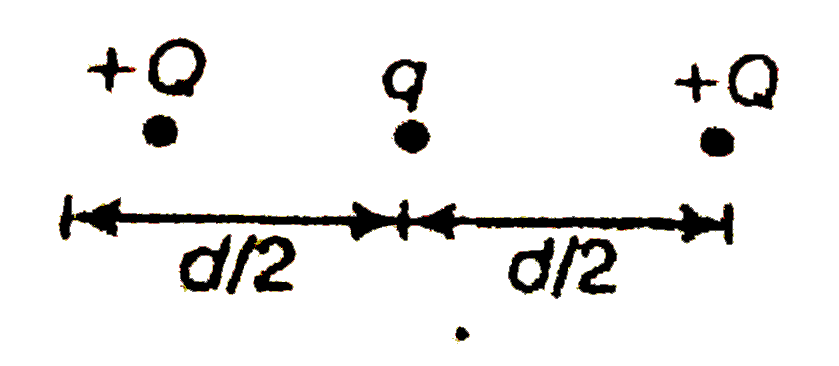 Aq=Q4Bq=Q4Cq=3Q4Dq=−3Q4
Aq=Q4Bq=Q4Cq=3Q4Dq=−3Q4A point charge q of mass m is located at the centre of a ring having radius R and charge Q. When it is displaced slightly, the point charge accelerates along the x-axis to infinity, the ultimate speed of the point charge :-
A√2kQqmRB√kQqmRC√kQq2mRDzero
Two point charges+ q and-q are placed at distanced apart. What are the points at which the resultant field is parallel to the line joining the two charges ?
View SolutionTwo infinitely long line charges having charge density λ each are parallel to each other and separated by distance d. A charge particle of mass m and charge q is placed at mid point between them. This charge displaced slightly along a line AB which is perpendicular to the line charges and in the plane of the charges. prove that the motion of the particle will be SHM for small displacement and λq>0 Neglect gravity. Find the time period.
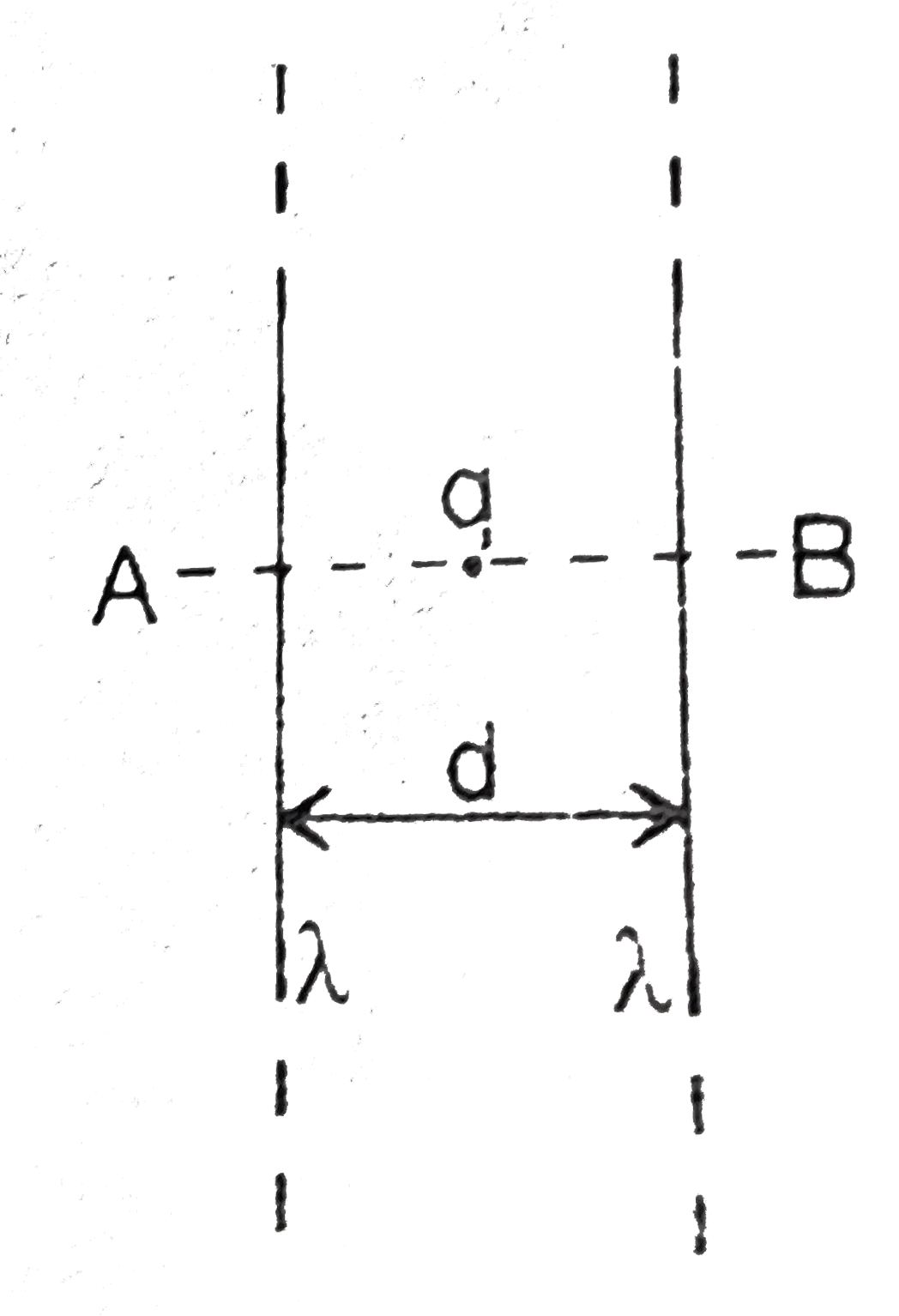
View SolutionTwo points charges , each Q , are fixed at separation 2d. A charged particle having charge q and mass m is placed between them.
(a) Now this charged particle is slightly displaced along the line joining the charges , slow that it will execute simple harmonic motion and find the time period of oscillation.
(b) If charge q is negative and it is displaced slightly perpendicular to the line joining the charges , repeat the part (a).
View SolutionTwo equal charges, +Q each, are at a distance r from each other. A third charge is placed on the line joining the above two charges such that all these charges are in equilibrium. Find q, in terms of Q.
View SolutionTwo stationary particles each of +q are placed at a distacne apart. Now a negatively charged particle is placed in a straight line joining two charge. The direction of motion of the negatively charged particle will depend on
View Solution
