A solid sphere of radius R1 and volume charge density ρ=ρ0r is enclosed by a hollow sphere of radius R2 with negative surface charge density σ, such that the total charge in the system is zero . ρ0 is positive constant and r is the distance from the centre of the sphere . The ratio R2/R1 is
σ/R0
√2σ/ρ0
√ρ0/2σ
ρ0/σ
The correct Answer is:C
Total charge in the inner sphere
Q1=∫R10ρdV=∫R10ρ0r(4πr2)dr=4πR212ρ0
Total charge on outer shell
Q2=−4πR22σ
Since, Q1+Q2=0
4πR212ρ0=4πR22σ⇒R22R12=ρ02σ⇒R2R1=√ρ02σ
Topper's Solved these Questions
- ELECTROSTATICSBOOK - ERRORLESSCHAPTER - ELECTROSTATICSEXERCISE - NCERT BASED QUESTIONS (Electric Field and Potential)
129 Videos
- ELECTROSTATICSBOOK - ERRORLESSCHAPTER - ELECTROSTATICSEXERCISE - NCERT BASED QUESTIONS (Electric Dipole)
21 Videos
- ELECTRONICSBOOK - ERRORLESSCHAPTER - ELECTRONICSEXERCISE - Assertion & Reason
26 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - ERRORLESSCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - ASSERTION & REASON
18 Videos
Similar Questions
Repeat the question if sphere is a hollow non-conducting sphere of radius R and has uniform surface charge density σ.
View SolutionA sphere of radius R_(0 carries a volume charge density proportional to the distance (x) from the origin, rho=alpha x where alpha is a positive constant.The total charge in the sphere of radius R_(0) is
View Solution
Knowledge Check
Two charged spheres of radii R1andR2 having equal surface charge density. The ratio of their potential is
AR1/R2BR2/R1C(R1/R2)2D(R2/R1)2An insulating solid sphere of the radius R is charged in a non - uniform manner such that the volume charge density ρ=Ar, where A is a positive constant and r is the distance from the centre. The potential difference between the centre and surface of the sphere is
AAR8ε0BAR4ε0CARε0DAR2ε0For the hemisphere of radius R shown in the figure the surface charge density σ varies with θ (shown in figure) as σ=σ0cosθ the total charge on the sphere is
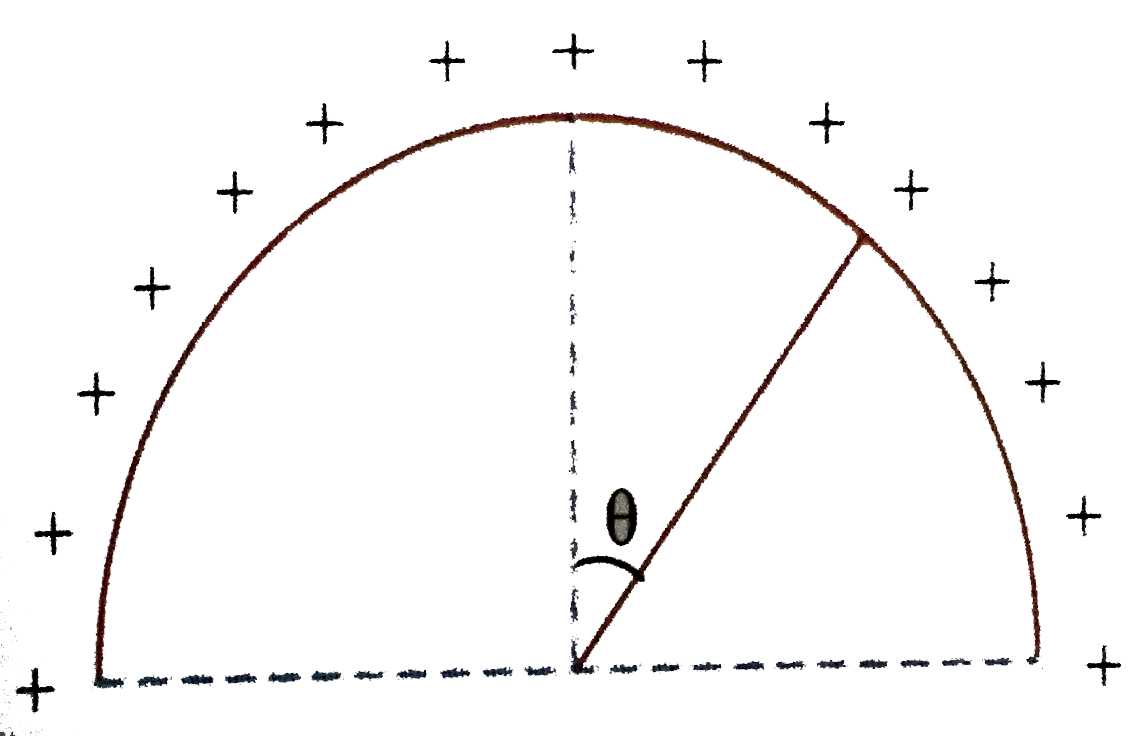 A2σ0πR2Bσ0πR22Cσ0πR23Dσ0πR2
A2σ0πR2Bσ0πR22Cσ0πR23Dσ0πR2
A sphere of radius R contains charge density ρ(r)=A(R−r), for 0<r<R. The total electric charge inside the sphere is Q.
The value of A in terms of Q and R is
View SolutionA solid sphere of radius R has a charge Q distributed in its volume with a charge density ρ=kra, where k and a are constants and r is the distance from its centre. If the electric field at r=R2 is 18 times that r=R, find the value of a.
View SolutionAn insulating solid sphere of the radius R is charged in a non - uniform manner such that the volume charge density ρ=Ar, where A is a positive constant and r is the distance from the centre. The potential difference between the centre and surface of the sphere is
View SolutionThe electric field intensity in free space at a distance 'r' outside a charged conducting sphere of radius 'R' in terms of surface charge density σ is
View SolutionA solid sphere of radius R has a volume charge density ρ=ρ0r2 (where ρ0 is a constant ans r is the distance from centre). At a distance x from its centre (for x<R), the electric field is directly proportional to :
View Solution
