Moment of inertia of a sphere of mass M and radius R is I. Keeping M constant if a graph is plotted between I and R, then its form would be

A

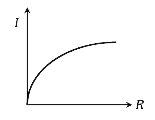
ocr_image

B

ocr_image

C

ocr_image

D

ocr_image

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

$I = \frac{2 M R^{2}}{3} \Rightarrow I \propto R^{2}$ [M=constant]
(Parabola)

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

BOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - NCERT BASED QUESTIONS (Angular Momentum)
52videos
ROTATIONAL MOTION
BOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - NCERT BASED QUESTIONS (Work, Energy and Power)
44videos
ROTATIONAL MOTION
BOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - NCERT BASED QUESTIONS (Angular Displacement, Velocity and Acceleration)
34videos
ROTATIONAL MOTION
BOOK - ERRORLESSCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - ASSERTION & REASON
18videos
NEWTON'S LAWS OF MOTION
BOOK - ERRORLESSCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assertion & Reason
15videos
SIMPLE HARMONIC MOTION

Similar Questions

Knowledge Check

Question 1 - Select One
Moment of inertia of a disc of mass 'M' and radius 'R' about the diameter is
A $\frac{M R^{2}}{2}$
B $\frac{M R^{2}}{4}$
C $\frac{M R^{2}}{3}$
D $\frac{M R^{2}}{12}$
Question 2 - Select One
Moment of inertia of a circular wire of mass M and radius R about its diameter is
A $M \frac{R^{2}}{2}$
B $M R^{2}$
C $2 M R^{2}$
D $M \frac{R^{2}}{4}$
Question 3 - Select One
Moment of inertia of a circular wire of mass $M$ and radius $R$ about its diameter is :
A $\frac{M R^{2}}{2}$
B $M R^{2}$
C $2 M R^{2}$
D $\frac{M R^{2}}{4}$

ERRORLESS-ROTATIONAL MOTION-NCERT BASED QUESTIONS (Moment of Inertia)

Home
Ask Doubt
Profile