Three bricks each of length L and mass M are arranged as shown from the wall. The distance of the centre of mass of the system from the wall is

L/4
L/2
(3/2)L
(5/6)L
The correct Answer is:D
m1=m2=m3=M
x1=L/2,x2=L,x3=L+L4=5L4
xCM=m1x1+m2x2+m3x3m1+m2+m3
= M×(L2+L+5L4)3M=11L12
Topper's Solved these Questions
- ROTATIONAL MOTIONBook:ERRORLESSChapter:ROTATIONAL MOTIONExercise:NCERT BASED QUESTIONS (Angular Displacement, Velocity and Acceleration)
Explore 34 Videos
- ROTATIONAL MOTIONBook:ERRORLESSChapter:ROTATIONAL MOTIONExercise:NCERT BASED QUESTIONS (Moment of Inertia)
Explore 139 Videos
- NEWTON'S LAWS OF MOTIONBook:ERRORLESSChapter:NEWTON'S LAWS OF MOTIONExercise:ASSERTION & REASON
Explore 18 Videos
- SIMPLE HARMONIC MOTIONBook:ERRORLESSChapter:SIMPLE HARMONIC MOTIONExercise:Assertion & Reason
Explore 15 Videos
Similar Questions
Two uniform thin rods each of length L and mass m are joined as shown in the figure. Find the distance of centre of mass the system from point O

View SolutionSix rods of the same mass m and length ? are arranged as shown in figure. Calculate the coordinate of the centre of mass of the system:- У >X
View Solution
Knowledge Check
Two point masses m and M are separated bya distance L . The distance of the centre of mass of the system from m is
AL(m/M)BL(M/m)CL(Mm+M)DL(mm+M)Two point masses m and M are separated by a distance L . The distance of the centre of mass of the system from m is
AL(m/M)BL(M/m)CL(Mm+M)DL(mm+M)Three rings each of mass M and radius R are arranged as shown in the figure. The moment of inertia of the system about YY¢ will be
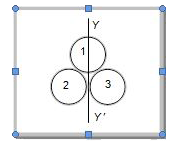 A3MR2B32MR2C5MR2D72MR2
A3MR2B32MR2C5MR2D72MR2
The mass per unit length of a non- uniform rod OP of length L varies as m=k(x)/(L) where k is a constant and x is the distance of any point on the rod from end 0 .The distance of the centre of mass of the rod from end 0 is
View SolutionTwo bodies of masses m1 and m2 are separated by a distance R. The distance of the centre of mass of the bodies from the mass m1 is
View SolutionTwo bodies of masses m1 and m2 are separated by a distance R. The distance of the centre of mass of the bodies from the mass m1 is
View SolutionThree identical particles each of mass 0.1kg are arranged at three corners of a square of side √2m. The distance of the centre of mass from the fourth corners is
View SolutionA thin uniform rod of length L is bent at its mid point as shown in the figure. The distance of the centre of mass from the point O is

View Solution