A circular disk of moment of inertia $I_{t}$ is rotating in a horizontal plane, about its symmetry axis, with a constant angular speed $ω_{i}$ Another disk of moment of inertia $I_{b}$ is dropped coaxially onto the rotating disk. Initially the second disk has zero angular speed. Eventually both the disks rotate with a constant angular speed $ω_{f}$ The energy lost by the initially rotating disc to friction is

$\frac{1}{2} \frac{I_{b} I_{t}}{(I_{t} + I_{b})} ω_{1}^{2}$

$\frac{1}{2} \frac{I_{b}^{2}}{(I_{t} + I_{b})} ω_{1}^{2}$

$\frac{1}{2} \frac{I_{t}^{2}}{(I_{t} + I_{b})} ω_{1}^{2}$

$\frac{I_{b} - I_{t}}{(I_{t} + I_{b})} ω_{1}^{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

$I_{t} ω_{i} = (I_{t} + I_{b}) ω_{f}, ω_{f} = (I_{9} t) ω_{i} \frac{)}{I_{t} + I_{b}}$
$K_{i} = \frac{1}{2} I_{t} ω_{i}^{2}$
$K_{f} = \frac{1}{2} (I_{t} + I_{b}) ω_{f}^{2}$
loss of energy $= K_{i} - K_{f}$
$= \frac{1}{2} I_{t} ω_{i}^{2} - \frac{1}{2} {(\frac{I_{t} ω_{i}}{I_{t} + I_{b}})}^{2} (I_{t} + I_{b})$
$= \frac{1}{2} I_{t} ω_{i}^{2} [1 - \frac{I_{t}}{I_{t} + I_{b}}] = \frac{1}{2} (\frac{I_{b} I_{t}}{I_{b} + I_{t}}) ω_{i}^{2}$

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
A disc of the moment of inertia $' l_{1}'$ is rotating in horizontal plane about an axis passing through a centre and perpendicular to its plane with constant angular speed $' ω_{1}'$ . Another disc of moment of inertia $' I_{2}'$ . having zero angular speed is placed discs are rotating disc. Now, both the discs are rotating with constant angular speed $' ω_{2}'$ . The energy lost by the initial rotating disc is
A $\frac{1}{2} [\frac{l_{1} + l_{2}}{l_{1} l_{2}}] ω_{1}^{2}$
B $\frac{1}{2} [\frac{l_{1} l_{2}}{l_{1} - l_{2}}] ω_{1}^{2}$
C $\frac{1}{2} [\frac{l_{1} - l_{2}}{l_{1} l_{2}}] ω_{1}^{2}$
D $\frac{1}{2} [\frac{l_{2} l_{2}}{l_{1} + l_{2}}] ω_{1}^{2}$
Question 2 - Select One
A disc of moment of inertia $I_{1}$ is rotating freely with angular speed $ω_{1}$ when another non-rotating disc of moment of inertia $I_{2}$ is dropped on it. The two discs then rotate as one unit. Find the final angular speed.
A $\frac{I_{1} ω_{1}}{I_{2}}$
B $\frac{I_{2} ω_{1}}{I_{2} + I_{2}}$
C $\frac{I_{1} ω_{2}}{I_{1} + I_{2}}$
D $\frac{(I_{1} + I_{2})}{I_{2} ω_{1}}$
Question 3 - Select One
A disk with moment of inertia $I_{1}$ rotates about frictionless, vertical axle with angular speed $ω_{i}$ A second disk, this one having moment of inertia $I_{2}$ and initial not rotating, drops onto the first disk (Fig.) Because of friction between the surfaces, the two eventually reach the same angular speed $ω_{f}$ . The value of $ω_{f}$ is.
.
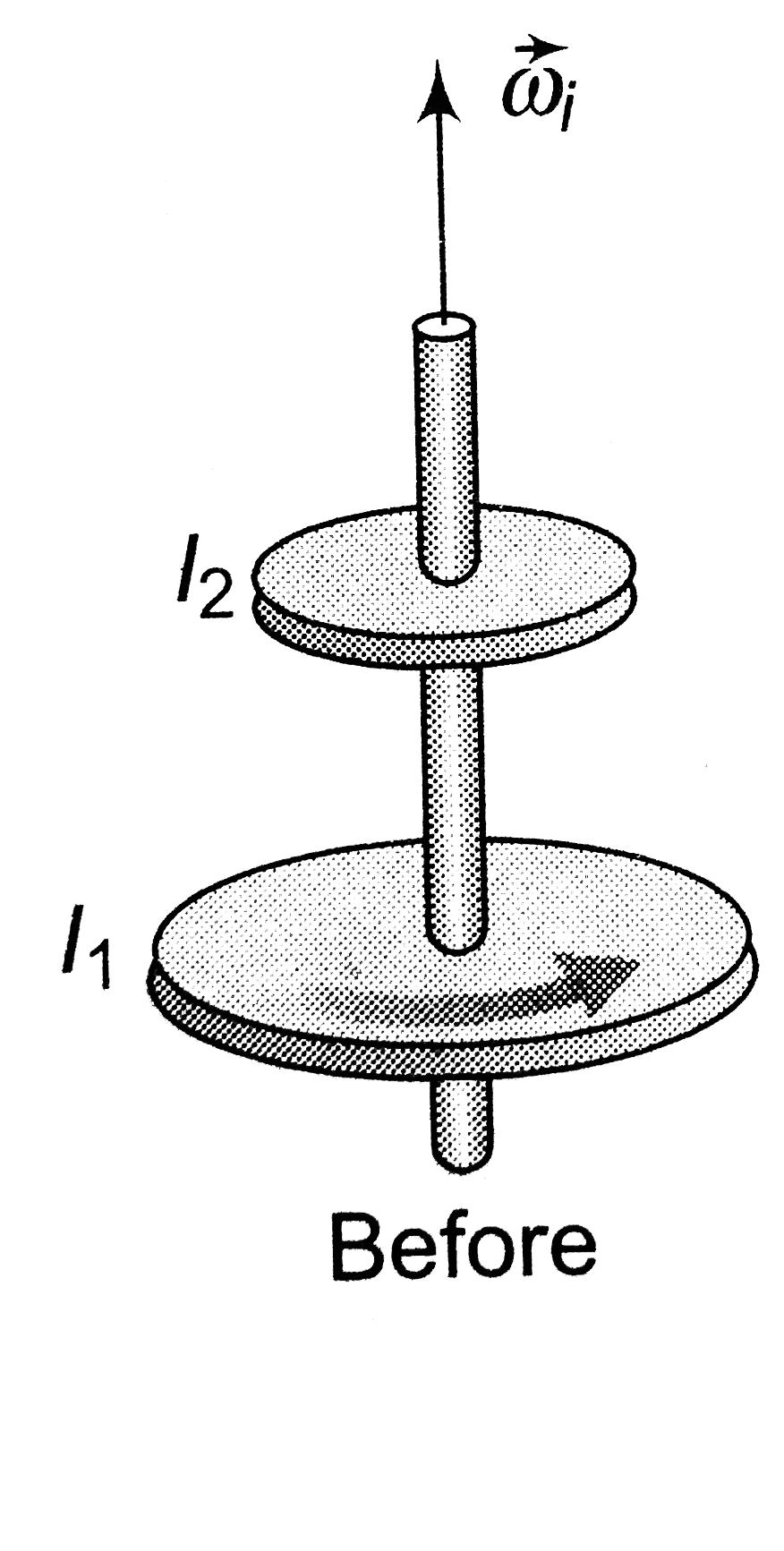A $\frac{I_{1} + I_{2}}{I_{1}} ω_{i}$
B $\frac{I_{1}}{I_{1} + I_{2}} ω_{i}$
C $\frac{I_{1} + I_{2}}{I_{2}} ω_{i}$
D $\frac{I_{1}}{I_{2}} ω_{i}$

ERRORLESS-ROTATIONAL MOTION-NCERT BASED QUESTIONS (Work, Energy and Power)

Home
Ask Doubt
Profile

The correct Answer is:A

Itωi=(It+Ib)ωf,ωf=(I9t)ωi)It+Ib Ki=12Itω2i Kf=12(It+Ib)ω2f loss of energy =Ki−Kf =12Itω2i−12(ItωiIt+Ib)2(It+Ib) =12Itω2i[1−ItIt+Ib]=12(IbItIb+It)ω2i

Topper's Solved these Questions

Similar Questions

Knowledge Check

A disc of moment of inertia I1 is rotating freely with angular speed ω1 when another non-rotating disc of moment of inertia I2 is dropped on it. The two discs then rotate as one unit. Find the final angular speed.

ERRORLESS-ROTATIONAL MOTION-NCERT BASED QUESTIONS (Work, Energy and Power)

A disc of moment of inertia $I_{1}$ is rotating freely with angular speed $ω_{1}$ when another non-rotating disc of moment of inertia $I_{2}$ is dropped on it. The two discs then rotate as one unit. Find the final angular speed.