A cricket bat is cut at the location of its centre of mass as shown, then

The two pieces will have the same mass
The bottom piece will have larger mass
The handle piece will have larger mass
Mass of handle piece is double the mass of bottom piece
The correct Answer is:B
Centre of mass will lie towards heavier side i.e. the bottom will have larger mass.
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - NCERT BASED QUESTIONS (Angular Displacement, Velocity and Acceleration)
34 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - NCERT BASED QUESTIONS (Moment of Inertia)
139 Videos
- NEWTON'S LAWS OF MOTIONBOOK - ERRORLESSCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - ASSERTION & REASON
18 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESSCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assertion & Reason
15 Videos
Similar Questions
Knowledge Check
A baseball bat of uniform density is cut at the location of its center of mass as shown in figure. The piece with the smaller mass is
 Athe piece on the rightBthe piece on the leftCBoth pieces have the same massDimpossible to determine.
Athe piece on the rightBthe piece on the leftCBoth pieces have the same massDimpossible to determine.What will be the position of centre of mass of a half disc shown ?
 .A2aπB4a3πCaπD2a3π
.A2aπB4a3πCaπD2a3πSelect the WRONG statement.
The location of centre of mass of a system of particlesAdepends on the masses of particles.Bdepends on the relative positions of the particles.Cdepends on the reference frame used to locate it.Ddoes not depend on the reference frame used.
The acceleration of centre of mass of system as shown in figure is
View SolutionFind the position of centre of mass of the section shown in figure

View Solutionconsider there particles connected by massless rods. Find the locations fo the centre of mass of the system of three particles as shown in fig 4E.36

View SolutionA square of side 4m having uniform thickness is divided into four equal squares as shown in Fig. If one of the squares is cut off, find
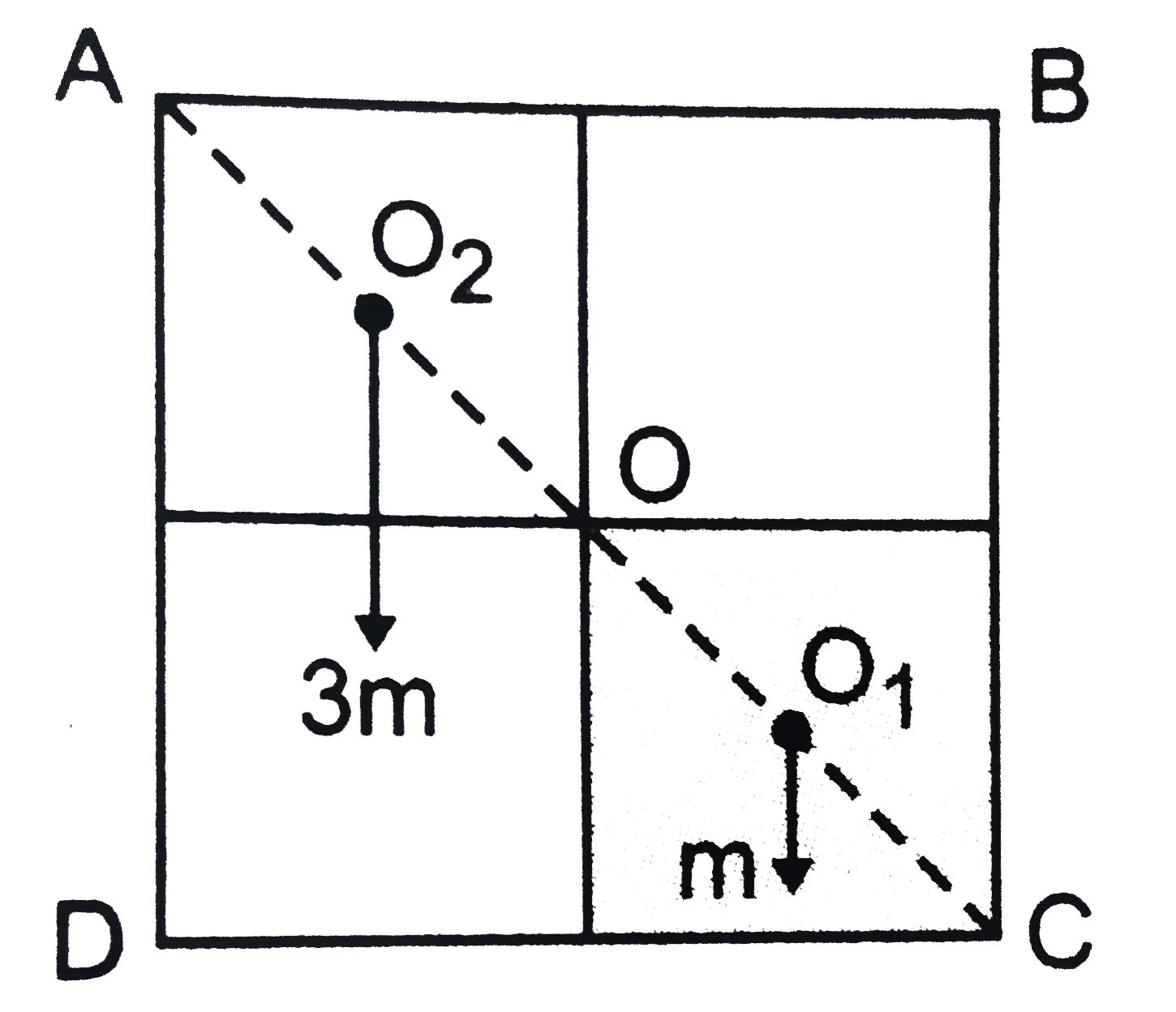
the position of centre of mass of the remaining portion from the centre O.
View SolutionFrom a solid cylined of length 4R and radius R, two hemispheres of radius R and R2 are cut from both the ends as shown. The location of new centre of mass from point O is approximately

View Solution


