A mass m rests on another mass M. The co-efficient of static friction between the surfaces of m and M is μ. M rests on smooth frictionless horizontal plane. The maximum force applied horizontally on M for which m will move along with M without slipping is
mg + μ mg
(M+m)μg
mMM+mμg
μmg
The correct Answer is:B
To solve the problem, we need to find the maximum force F that can be applied horizontally on mass M such that mass m moves along with M without slipping.
1. Identify Forces Acting on Mass m:
- The gravitational force acting on mass m is mg (downward).
- The normal force N exerted by mass M on mass m is equal to the gravitational force, hence N=mg.
- The static friction force fs acts to the right (opposing the relative motion) and is given by fs=μN.
2. Set Up the Equations:
- The maximum static friction force that can act on mass m is:
fs=μN=μmg
- For mass m to move along with mass M without slipping, the friction force must equal the net force required to accelerate mass m at the same acceleration a as mass M:
fs=ma
- Therefore, we have:
μmg=ma
3. Solve for Acceleration a:
- From the equation μmg=ma, we can cancel m (assuming m≠0):
a=μg
4. Determine the Force F on Mass M:
- The total force F applied to mass M must be equal to the total mass being accelerated (both M and m):
F=(M+m)a
- Substituting a=μg:
F=(M+m)(μg)
5. Final Expression for Maximum Force:
- Thus, the maximum force F that can be applied to mass M without causing mass m to slip is:
F=μg(M+m)
Conclusion:
The maximum force applied horizontally on M for which m will move along with M without slipping is:
F=μg(M+m)
- The gravitational force acting on mass m is mg (downward).
- The normal force N exerted by mass M on mass m is equal to the gravitational force, hence N=mg.
- The static friction force fs acts to the right (opposing the relative motion) and is given by fs=μN.
- The maximum static friction force that can act on mass m is:
fs=μN=μmg
- For mass m to move along with mass M without slipping, the friction force must equal the net force required to accelerate mass m at the same acceleration a as mass M:
fs=ma
- Therefore, we have:
μmg=ma
- From the equation μmg=ma, we can cancel m (assuming m≠0):
a=μg
- The total force F applied to mass M must be equal to the total mass being accelerated (both M and m):
F=(M+m)a
- Substituting a=μg:
F=(M+m)(μg)
- Thus, the maximum force F that can be applied to mass M without causing mass m to slip is:
F=μg(M+m)
The maximum force applied horizontally on M for which m will move along with M without slipping is:
F=μg(M+m)
Topper's Solved these Questions
- FRICTION BOOK - ERRORLESSCHAPTER - FRICTION EXERCISE - NCERT BASED QUESTIONS (Kinetic Friction )
20 Videos
- FRICTION BOOK - ERRORLESSCHAPTER - FRICTION EXERCISE - NCERT BASED QUESTIONS (Motion on Inclined Surface )
11 Videos
- FLUID MECHANICSBOOK - ERRORLESSCHAPTER - FLUID MECHANICSEXERCISE - ASSERTION AND REASON
23 Videos
- GRAVITATIONBOOK - ERRORLESSCHAPTER - GRAVITATIONEXERCISE - Assertion and Reason
25 Videos
Similar Questions
The coefficient of static friction between the two blocks shown in figure is μ and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?

View SolutionA block of mass m rests on a bracket of mass M. The coefficients of friction between block and bracket are μs and μk . The bracket rests on a frictionless surface. What is the maximum force F that can be applied if the block is not to slide on the bracket?
View Solution
Knowledge Check
A bar of mass m1 is placed on a plank of mass m2 which rests on a smooth horizontal plane . The coefficient of friction between the surfaces of bar and plank is k . The plank is subjected to a horizontal force F depending on time t as F = at , where a is a constant . The moment of time t0 at which the plank starts sliding is :
 Aakgm1+m2B(m1+m2)kgaC(m1+m2)gkaDka(m1+m2)g
Aakgm1+m2B(m1+m2)kgaC(m1+m2)gkaDka(m1+m2)gA block of mass m is placed at rest on an inclination θ to the horizontal.If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
AmgBμmgcosθCmgsinθDμmgtanθA block of massm is placed on another block of mass M which itself is lying on a horizontal surface .The coefficient of friction between two blocks is μ1and that between the block of mass M and horizontal surfece is μ2 What maximum horizontal force can be applied to the lower block move without separation?
 A(M+m)(μ2−μ1)gB(M−m)(μ2−μ1)gC(M−m)(μ2+μ1)gD(M+m)(μ2+μ1)g
A(M+m)(μ2−μ1)gB(M−m)(μ2−μ1)gC(M−m)(μ2+μ1)gD(M+m)(μ2+μ1)g
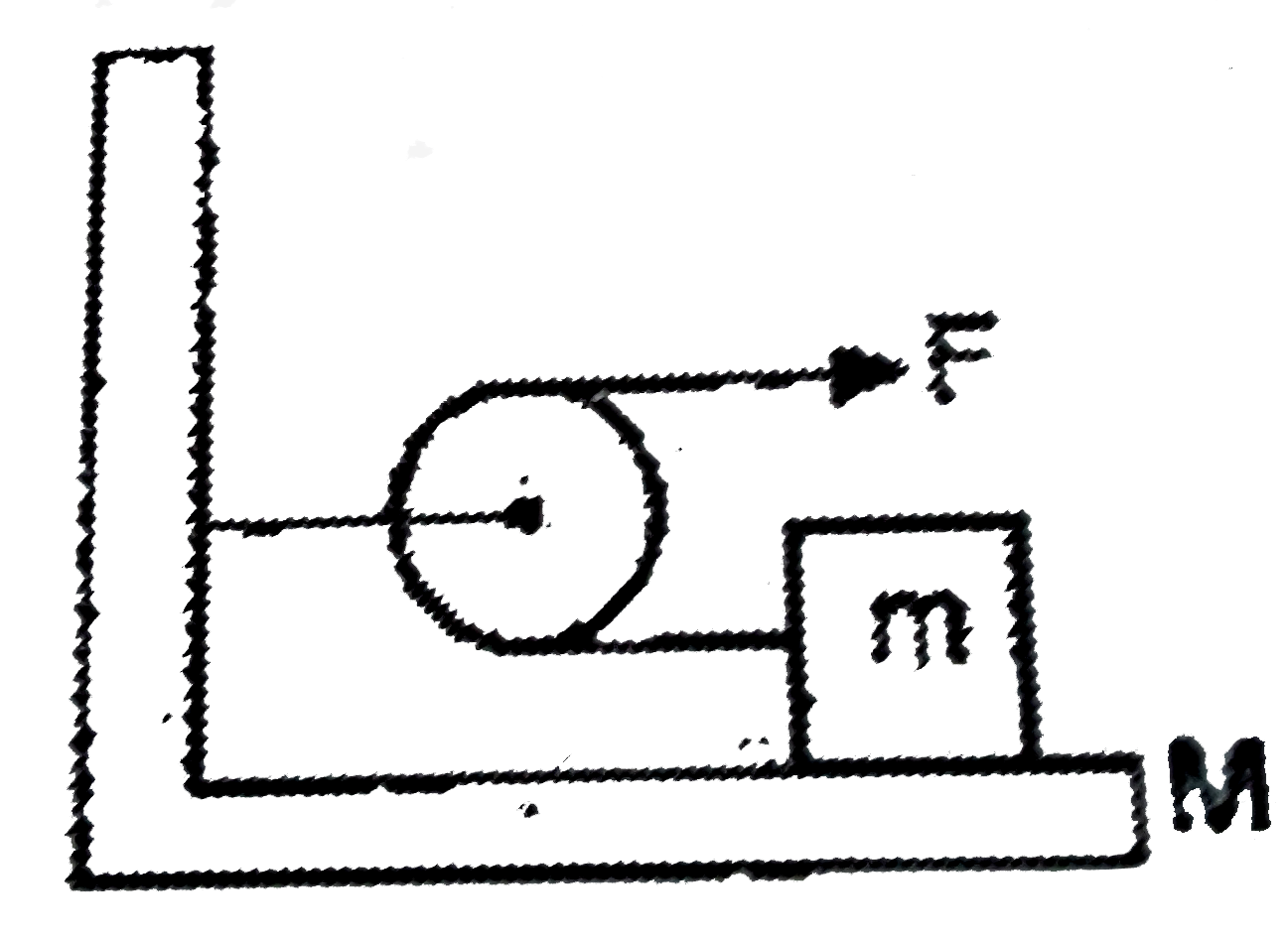
A small block of mass 'm' is placed on a plank of mass 'M'. The block is connected to plank with the help of a light string passing over a light smooth pulley as shown in figure. The co-efficient of static friction between the block and plank is μ.
The co-efficient of friction between the plank and the horizontal surface is zero. What maximum horizontal force F applied on the block of mass m can make the block and plank not to slide relatively?
View SolutionTwo blocks of masses M1 and M2 connected by a light spring rest on a horizontal plane . The coefficient of friction between the blocks and the surface is equal to μ . The minimum constant force that has to be applied in the horizontal direction to the block of mass M1 in order to shift the other block is (M1+M2α)μg , then α is :
View SolutionA block of mass m is kept over another block of mass 2m. Coefficient of friction between two blocks is μ and that of between lower blood from the horizontal surface is zero. A horizontal force F=43μmg is applied on the block of mass 2m. Acceleration of lower block is
View SolutionIn figure-2.86, the blockA of mass M1 rests on a rough horizontal surface. The coefficient of friction between the block and the surface is μ. A uniform plank B, of mass M2 rests on A. B is prevented from moving by connecting it to a light rod R which is hinged at one end H.The coefficient of friction between A and B is μ. Findthe acceleration of blocks A and C.

[M3g−μg(M1+2M2)(M1+M3)]
View SolutionA block of mass m is placed on the top of another block of mass M as shown in the figure. The coefficient of friction between them is μ.

The maximum acceleration with which the block M may move so that m also moves along with it is
View Solution
