A pen of mass 'm' is lying on a piece of paper of mass M placed on a rough table. If the coefficient of friction between the pen and paper, and, the paper and table are μ1 and μ2, respectively, then the minimum horizontal force with which the paper has to be pulled for the pen to start slipping is given by-
(m+M)(μ1+μ2)g
(mμ1+Mμ2)g
{mμ1+(m+M)μ2}g
m(μ1+μ2)g
The correct Answer is:A
For pen to start slipping maximum horizontal force on it is f=μ1mg
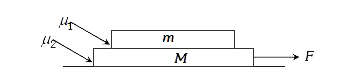
∴a=μ1g is the maximum common acceleration for both pen and paper .
F , B , D for both pen and paper
f1=μ1N1 and N1=W1
∴f1=μ1mg
∴N2=N1+W2
F−f1−f2= Ma
also f2=μ2N2=μ2(m+M)g ∴F=f1+f2 + Ma
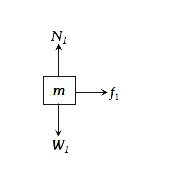
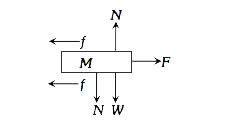
F=μmg+μ2(m+M)g+M(μ1g)
F=(m+M)(μ1+μ2)g
Topper's Solved these Questions
- FRICTION Book:ERRORLESSChapter:FRICTION Exercise:NCERT BASED QUESTIONS (Kinetic Friction )
Explore 20 Videos
- FRICTION Book:ERRORLESSChapter:FRICTION Exercise:NCERT BASED QUESTIONS (Motion on Inclined Surface )
Explore 11 Videos
- FLUID MECHANICSBook:ERRORLESSChapter:FLUID MECHANICSExercise:ASSERTION AND REASON
Explore 23 Videos
- GRAVITATIONBook:ERRORLESSChapter:GRAVITATIONExercise:Assertion and Reason
Explore 25 Videos
Similar Questions
A vehicle of mass m is moving on a rough horizontal road with momentum p. If the coefficient of friction between the tyres and the road be μ, then the stopping distance is
View SolutionA vehicle of mass m is moving on a rough horizontal road with momentum P . If the coefficient of friction between the tyres and the road br mu, then the stopping distance is:
View Solution
Knowledge Check
A sphere of mass m and radius R is kept on a trolley of mass Mas shown in the figure. The coefficient of static and kinetic friction between the sphere and the trolley are μsandμk respectively. The maximum horizontal force F that can be applied to the trolley for which the solid sphere does not slip is
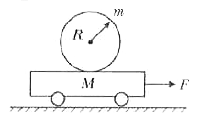 Aμsg(+72M)Bμkg(+72M)Cμsg(+52M)D92μsmg
Aμsg(+72M)Bμkg(+72M)Cμsg(+52M)D92μsmgA body of mass m kept on the floor of a lift moving downwards is pulled horizontally. If μ is the coefficient of friction between the surface in contact, then
Africtional resistance offered by the floor is 2 μmg, when lift moves up with a uniform velocity of 5 m/s.Brictional resistance offered by the floor is μumg, when lift moves lift moves up with uniform velocity of 3 m/s.Cfrictional resistance offered by the floor is 4.8μmg, when lift accelerates down with an acceleration of 4.8m/s2Dfrictional resistance offered by the floor must lie in the range 0≤f<∞A vehicle of mass M is moving on a rough horizontal road with a momentum P. If the coefficient of friction between the tyres and the road is μ, then the stopping distance is
AP2μMgBP22μMgCP22μM2gDP2μM2g
A vehicle of mass M is moving on a rough horizontal road with a momentum P If the coefficient of friction between the tyres and the road is μ is then the stopping distance is .
View SolutionA block of mass m is pulled by a force of constant power P placed on a rough horizontal plane. The friction coefficient between the block and the surface is μ. Then
View SolutionA body of mass m is placed on a rough surface with coefficient of friction μ inclined at θ. If the mass is in equilibrium , then
View SolutionA block of mass m is placed on a rough floor of a lift . The coefficient of friction between the block and the floor is μ. When the lift falls freely, the block is pulled horizontally on the floor. What is the force of friction -
View SolutionIf, in Q.19, coefficient of friction between m1 and the wall is μ,and f1 and f2 are respectively, the force of friction on m1 and m2, then :
View Solution