The work done by a force →F=(−6×x3ˆi)N in displacing a particle from x = 4 m to x = - 2 m is
360 J
240 J
−240J
−360J
The correct Answer is:A
To find the work done by the force →F=−6x3^i in displacing a particle from x=4m to x=−2m, we can follow these steps:
Step 1: Understand the Work Done Formula
The work done W by a variable force is given by the integral of the force over the displacement:
W=∫x2x1→F⋅d→x
Here, d→x=dx^i since the motion is along the x-axis.
Step 2: Set Up the Integral
Given the force →F=−6x3^i, we can set up the integral for work done as:
W=∫−24(−6x3)dx
Step 3: Change the Limits of Integration
Since we are integrating from x=4 to x=−2, we can rewrite the integral:
W=−6∫−24x3dx
To make the integration easier, we can switch the limits and change the sign:
W=6∫4−2x3dx
Step 4: Calculate the Integral
Now we compute the integral:
∫x3dx=x44
Thus,
W=6(x44)4−2
Step 5: Evaluate the Integral at the Limits
Now we evaluate the integral at the limits:
W=6(444−(−2)44)
Calculating 44 and (−2)4:
44=256and(−2)4=16
Substituting these values back:
W=6(2564−164)=6(64−4)=6×60
Step 6: Final Calculation
Now calculate:
W=360Joules
Conclusion
The work done by the force in displacing the particle from x=4m to x=−2m is:
360J
The work done W by a variable force is given by the integral of the force over the displacement:
W=∫x2x1→F⋅d→x
Here, d→x=dx^i since the motion is along the x-axis.
Given the force →F=−6x3^i, we can set up the integral for work done as:
W=∫−24(−6x3)dx
Since we are integrating from x=4 to x=−2, we can rewrite the integral:
W=−6∫−24x3dx
To make the integration easier, we can switch the limits and change the sign:
W=6∫4−2x3dx
Now we compute the integral:
∫x3dx=x44
Thus,
W=6(x44)4−2
Now we evaluate the integral at the limits:
W=6(444−(−2)44)
Calculating 44 and (−2)4:
44=256and(−2)4=16
Substituting these values back:
W=6(2564−164)=6(64−4)=6×60
Now calculate:
W=360Joules
The work done by the force in displacing the particle from x=4m to x=−2m is:
360J
Topper's Solved these Questions
- WORK, ENERGY POWER AND COLLISIONBOOK - ERRORLESSCHAPTER - WORK, ENERGY POWER AND COLLISIONEXERCISE - NCERT BASED QUESTIONS (Conservation of Energy and Momentum)
64 Videos
- WORK, ENERGY POWER AND COLLISIONBOOK - ERRORLESSCHAPTER - WORK, ENERGY POWER AND COLLISIONEXERCISE - NCERT BASED QUESTIONS (Power)
18 Videos
- WORK, ENERGY POWER AND COLLISIONBOOK - ERRORLESSCHAPTER - WORK, ENERGY POWER AND COLLISIONEXERCISE - ASSERTION & REASON
22 Videos
- WAVES AND SOUND BOOK - ERRORLESSCHAPTER - WAVES AND SOUND EXERCISE - ASSERTION & REASON
25 Videos
Similar Questions
A force (F) acting on a particle varoes work done by a particle varies with the with the position x as shown in figure
 .
.
Find the work done by by force in displacing the particle from .
(a) x=−2m to x=0
(b) x=0 to x=2m..
View SolutionWhen a force →F=(6ˆi−2ˆj) N displaces a particle by →S=(2ˆi−3ˆj) m, then average power is 0.4w. The time of action of force is
View Solution
Knowledge Check
The work done by a force →F=(−6x3ˆi) N in displacing a particle from x = 4m to x = - 2m is
A−240JB360JC420JDwill depend upon the pathA force F acting on a particle varies with the position x as shown in the graph. Find the work done by the force in displacing the particle from x=−a to x=+2a.
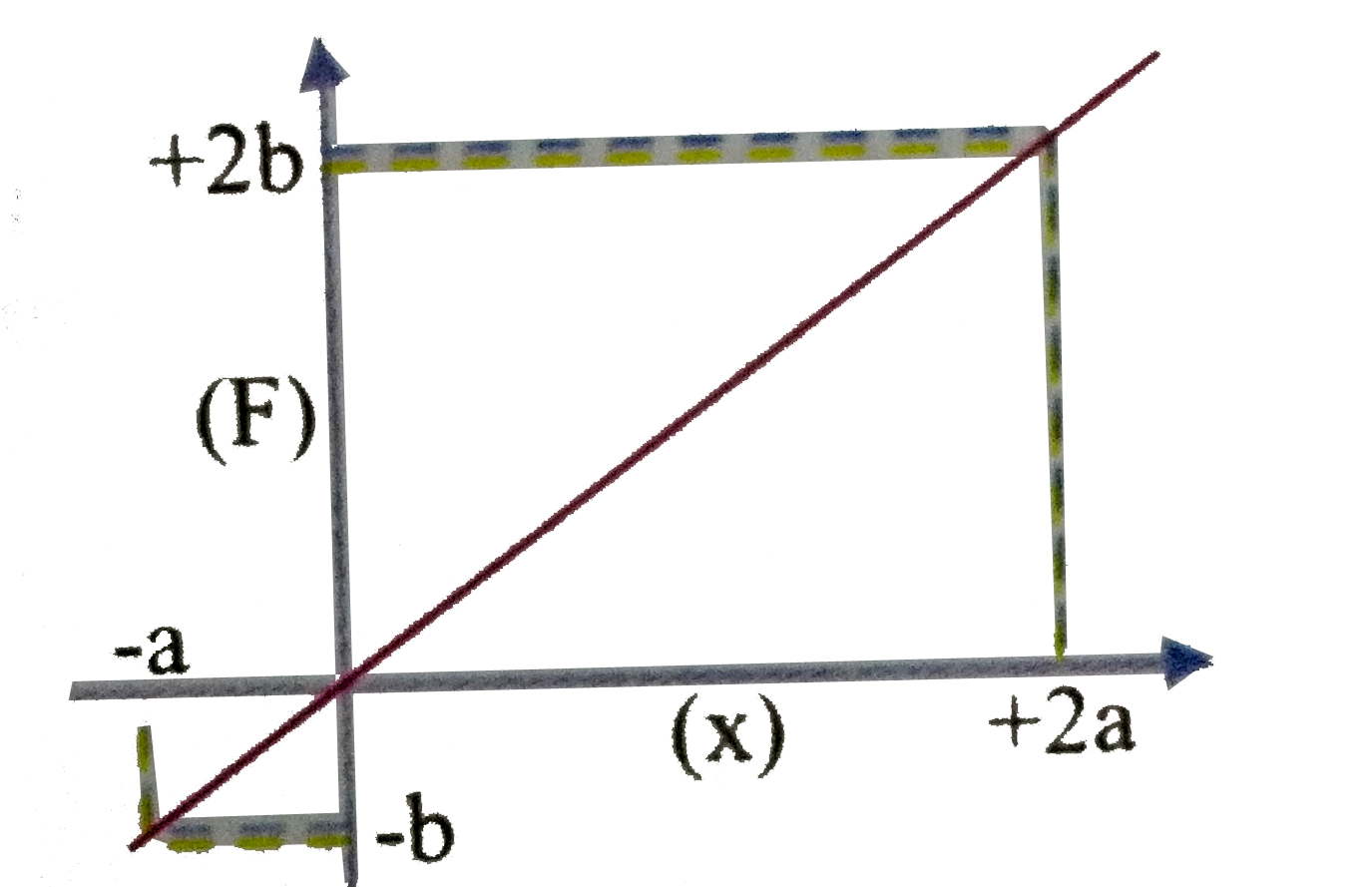 .A3ab2B4ab2C23abD24ab
.A3ab2B4ab2C23abD24abA force of F=(0.5x+12)N acts on a particle. If x is in metre, calculate the work done by the force during the displacement of the particle from x = 0 to x = 4 m
A128 JB80 JC64 JD52 J
A particle is acted upon by a force →F=yˆi+xˆj newton. When the particle is moved from (1 m, 1 m) to (9m, 3 m) via straight path, work done by →F is y. What is the value of xy?
View SolutionA particle of mass 2kg travels along a straight line with velocity v=a√x, where a is a constant. The work done by net force during the displacement of particle from x=0 to x=4m is
View SolutionA force Fy=(3x+2) N is acting on a body. The work done by this force if it tends to displace the body from x = 0 m to x = 4 m will be
View SolutionA force F = (2+ x)N acts on a particle in the x-direction. The work done by this force during a displacement from x = 1.0 m to x = 2.0 m is
View SolutionA force F is related to the position of a particle by the relation F=(10x2)N. The work done by the force when the particle moves from x= 2 m to x = 4 m is
View Solution
