A car is moving on a circular path and takes a turn. If R1 and R2 be the reactions on the inner and outer wheels, respectively, then
R1=R2
R1<R2
R1>R2
R1≥R2
The correct Answer is:B
Reaction on inner wheel R1=12M[g−v2hra]
Reaction on outer wheel R2=12M[g+v2hra]
r→ radius of circular path
2a→ distance between two wheel
h→ height of center of gravity of car.
Topper's Solved these Questions
- MOTION IN TWO DIMENSIONBOOK - ERRORLESSCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - NCERT BASED QUESTIONS (HORIZONTAL PROJECTILE MOTION)
11 Videos
- MOTION IN TWO DIMENSIONBOOK - ERRORLESSCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - NCERT BASED QUESTIONS (OBLIQUE PROJECTILE MOTION)
47 Videos
- MOTION IN TWO DIMENSIONBOOK - ERRORLESSCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - ASSERTION & REASON
19 Videos
- MOTION IN ONE DIMENSIONBOOK - ERRORLESSCHAPTER - MOTION IN ONE DIMENSIONEXERCISE - ASSERTION AND REASON
24 Videos
- NEWTON'S LAWS OF MOTIONBOOK - ERRORLESSCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - ASSERTION & REASON
18 Videos
Similar Questions
Knowledge Check
A car is moving on a circular path and takes a turn. If R1 and R2 be the reaction on the inner and outer wheels respectively, then
AR1=R2BR1<R2CR1>R2DR1≥R2The centre of gravity of a car is at a height h and the distance between its wheel is 2a. The car moves on a level curve of radius r with speed v. Let N1andN2 be the normal reactions on the inner and outer wheels of the car. Then
AN1>N2BN2>N1CN1=N2Dthe maximum value of v to avoid overturning is √arghWhen a car negotiates a curve, the normal force exerted on the inner and outer wheels are N2 and N1 respectively. Then N1/N2 is
A=1B<1C>1Dzero
A car of mass m travelling at speed v moves on a horizontal track. The centre of mass of the car describes a circle of radius r. If 2a is the separation of the inner and outer wheels and h is the height of the centre of mass above the ground, show that the limiting speed beyond which the car will overturn in given by
v2=grah
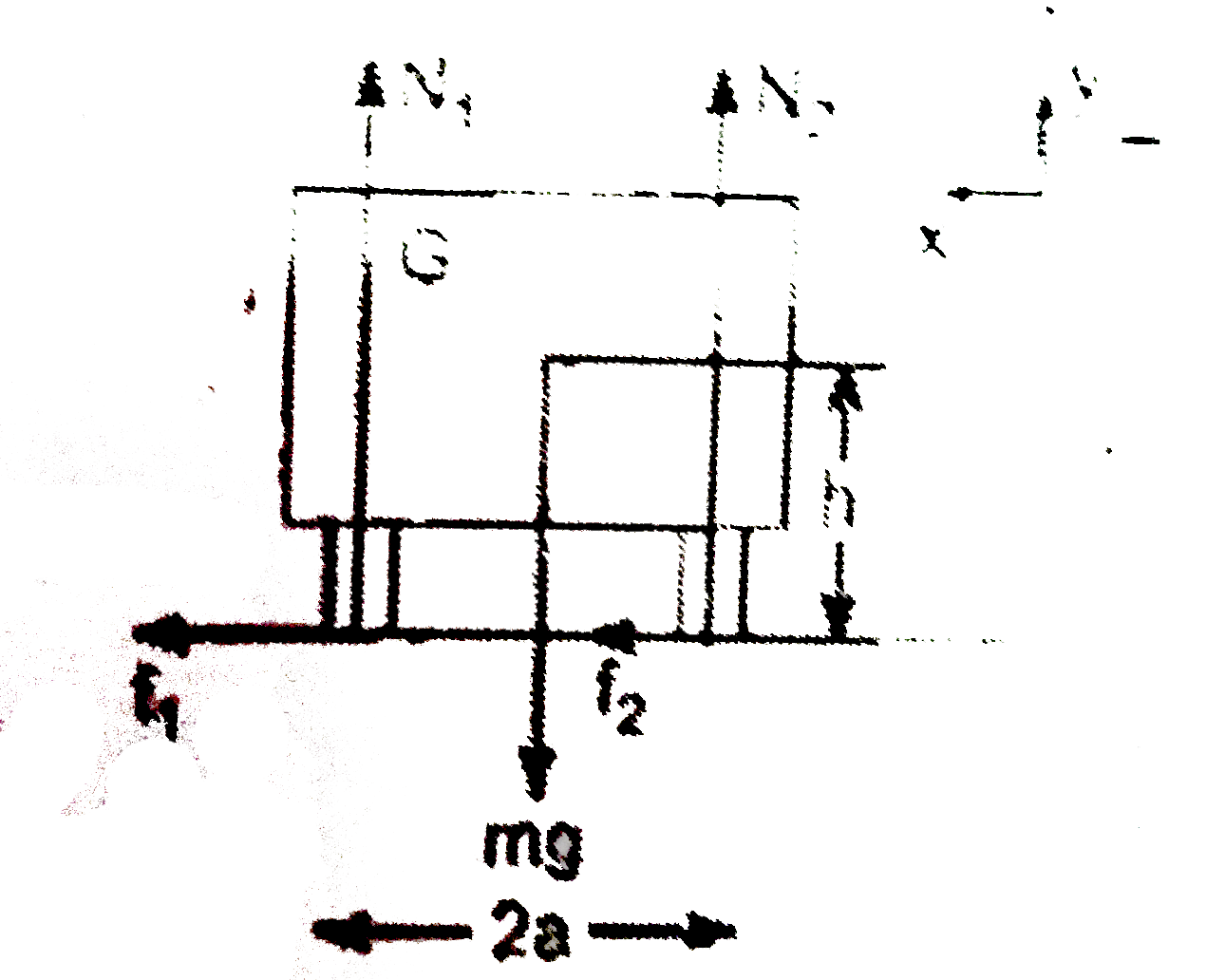
View SolutionA particle is moving around a circular path with uniform angular speed (x) . The radius of the circular path is (r). The acceleration of the particle is:
View SolutionA car is moving on a circular road which is rough and banked at angle . If radius of circular track is R then. Choose correct statement:
View SolutionA car is taking turn on a circular path of radius R. If the coefficient of friction between the tyres and road is μ, the maximum velocity for no slipping is
View SolutionA car moves with speed v on a horizontal circular track of radius R. A head-on view of the car is shown in figure. The height of the car's centre of mass above the ground is h, and the separation between its inner and outer wheels is d The road is dry, and the car does not skid. The maximum speed the car can have without overturning is :
 .
.
View Solution
