If ˆi,ˆj and ˆk represent unit vectors along the x, y and z axes respectively, then the angle θ between the vectors (ˆi+ˆj+ˆk) and (ˆi+ˆj) is equal to :
A
sin−1(1√3)
B
sin−1(√23)
C
cos−1(1√3)
D
90∘
Video Solution
Text Solution
The correct Answer is:A
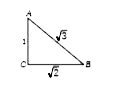
Since →A.→B=ABcosθ
⇒cosθ=→A.→BAB=(ˆi+ˆj+ˆk)(ˆi+ˆj)√12+12+12√12+12
⇒cosθ=2√6=√23
⇒sinθ=1√3
⇒θ=sin−1(1√3)
|
Topper's Solved these Questions
- BASIC MATHEMATICS AND VECTORSBOOK - ERRORLESSCHAPTER - BASIC MATHEMATICS AND VECTORSEXERCISE - NCERT Based Questions (Lami.s Theorem)
2 Videos
- BASIC MATHEMATICS AND VECTORSBOOK - ERRORLESSCHAPTER - BASIC MATHEMATICS AND VECTORSEXERCISE - Past Years Questions
12 Videos
- BASIC MATHEMATICS AND VECTORSBOOK - ERRORLESSCHAPTER - BASIC MATHEMATICS AND VECTORSEXERCISE - NCERT Based Questions (Addition and Subtraction of Vectors )
34 Videos
- ELASTICITYBOOK - ERRORLESSCHAPTER - ELASTICITYEXERCISE - ASSERTION & REASON
10 Videos
Similar Questions
Knowledge Check
If ˆi,ˆjandˆk are unit vectors along x,y and z-axis respectively, the angle θ between the vector ˆi+ˆj+ˆk and vectorˆj is given by
Aθ=cos−1(1√3)Bθ=sin−1(1√3)Cθ=cos−1(√32)Dθ=sin−1(√32)The angle between the vectors :
→a=ˆi+2ˆj−3ˆk and 3ˆi−ˆj+2ˆk is :Acos−1(514)Bcos−1(914)Ccos−1(−514)DNone of theseThe angle between the vectors (ˆi+ˆj+ˆk) and (ˆi−ˆj−ˆk) is
Asin−1(√83)Bsin−1(13)+π3Ccos−1(√83)Dcos−1√83
Find the angle between the vectors :
→a=ˆi+ˆj−ˆk and →b=ˆi−ˆj+ˆk
View SolutionThe angle between the vectors ˆi−ˆj and ˆj+ˆk is :
View SolutionAngle between the vectors (ˆi+ˆj)and (ˆj−ˆk) is
View SolutionThe angle θ between the vector →p=ˆi+ˆj+ˆk and unit vector along X-axis is
View SolutionThe angle between the Vector (ˆi+ˆj) and (ˆj+ˆk) is
View Solution
