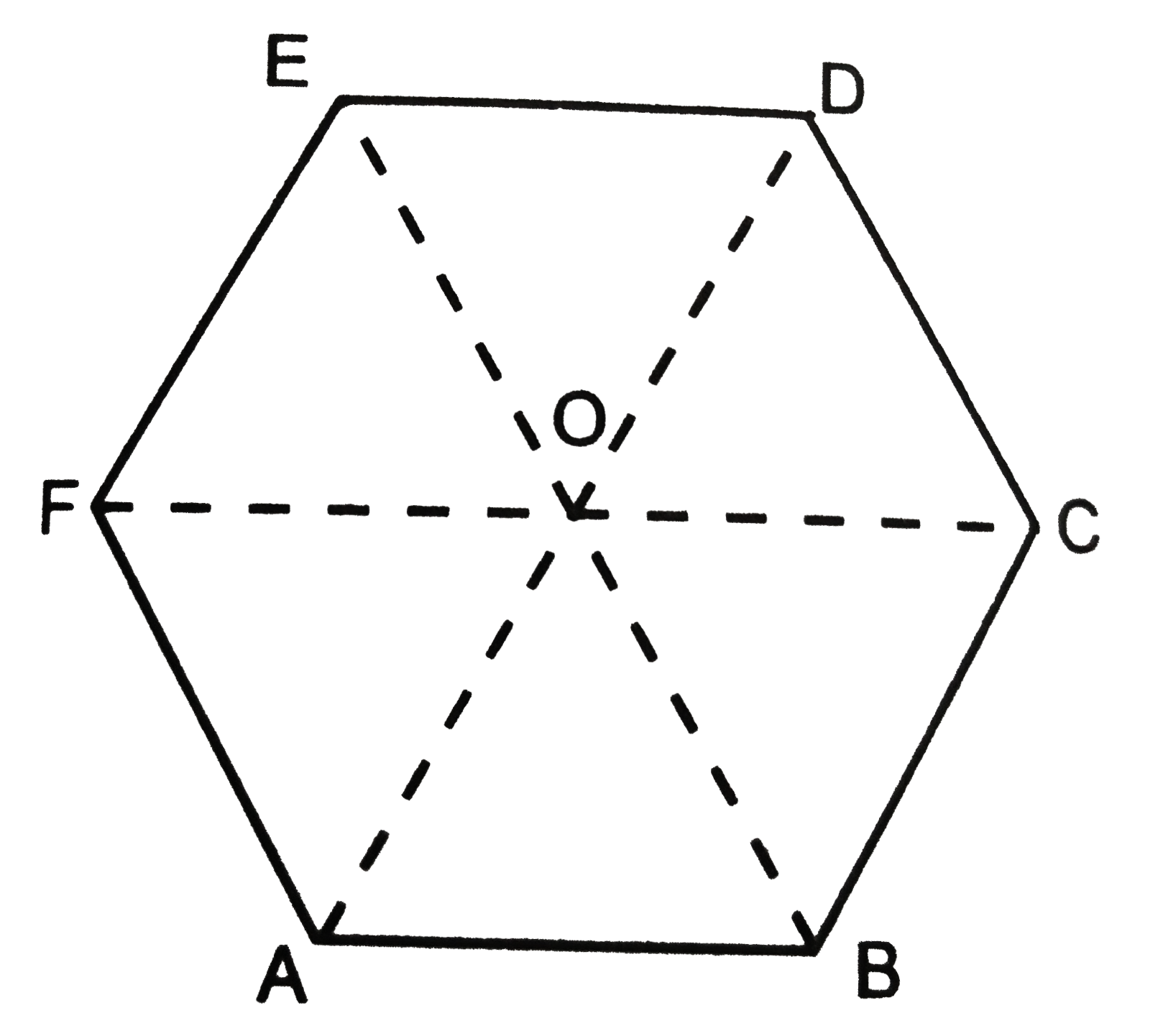
ABCDEF is a regular hexagon with point O as centre. The value of −−→AB+−−→AC+−−→AD+−−→AE+−−→AF is
A
−−→AO
B
2−−→AO
C
4−−→AO
D
6−−→AO
Video Solution
Text Solution
The correct Answer is:D
−−→AB+−−→AC+−−→AD+−−→AE+−−→AF=−−→OA+−−→OA+2−−→OA+−−→OA+−−→OA=6(−−→OA)=6(−−→AO)
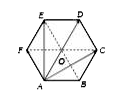
−−→AC=−−→AO
[angle between −−→ABand−−→BC is 120∘]

|
Topper's Solved these Questions
- BASIC MATHEMATICS AND VECTORSBOOK - ERRORLESSCHAPTER - BASIC MATHEMATICS AND VECTORSEXERCISE - NCERT Based Questions (Multiplication of Vectors )
23 Videos
- BASIC MATHEMATICS AND VECTORSBOOK - ERRORLESSCHAPTER - BASIC MATHEMATICS AND VECTORSEXERCISE - NCERT Based Questions (Lami.s Theorem)
2 Videos
- BASIC MATHEMATICS AND VECTORSBOOK - ERRORLESSCHAPTER - BASIC MATHEMATICS AND VECTORSEXERCISE - NCERT Based Questions (Fundamentals of Vectors)
25 Videos
- ELASTICITYBOOK - ERRORLESSCHAPTER - ELASTICITYEXERCISE - ASSERTION & REASON
10 Videos
Similar Questions
Knowledge Check
Consider the ragular hexagon ABCDEF with centre at O (origin).
Five forces −−→AB,−−→AC,−−→AD,−−→AE,−−→AF act at the vertex A of a regular hexagon ABCDEF. Then their resultant isA3−−→AOB2−−→AOC4−−→AOD6−−→AOLet O be the centre of a regular pentagon ABCDE and −−→OA=→a, then −−→AB+−−−→2BC+−−−→3CD+−−−→4DE+−−−→5EA is equals:
A0B4→aC5→aD6→aLet O be the centre of a regular pentagon ABCDE and −−→OA=→a, then −−→AB+−−−→2BC+−−−→3CD+−−−→4DE+−−−→5EA is equals:
A6→aB5→aC4→aD→0
ABCDEF is a regular hexagon with centre a the origin such that −−→AB+−−→EB+−−→FC=λ−−→ED then λ= (A) 2 (B) 4 (C) 6 (D) 3
View SolutionIf ABCDEF is a regular hexagon with −−→AB=→a and −−→BC=→b, then −−→CE equals
View SolutionABCDEF is a regular hexagon. Show that :
−−→OA+−−→OB+−−→OC+−−→OD+−−→OE+−−→OF=→0
View SolutionIf ABCDEF is a regular hexagon inscribed in a circle with centre O, then the value of ¯¯¯¯¯¯AB+¯¯¯¯¯¯AC+¯¯¯¯¯¯AD+¯¯¯¯¯¯AE+¯¯¯¯¯¯AF equals
View SolutionIn a regular hexagon ABCDEF, prove that −−→AB+−−→AC+−−→AD+−−→AE+−−→AF=3−−→AD
View Solution

 .
.