An average force of 900 N is applied to a 400 g steel ball moving at 15 m/s by a collision lasting 30 ms. If the force is in a direction opposite to the initial velocity of the ball then find the magnitude of final momentum of the ball.
6 kg m/s
21 kg m/s
33 kg m/s
27 kg m/s
The correct Answer is:B
To solve the problem, we need to find the final momentum of a steel ball after a force is applied in the opposite direction to its motion. Here’s a step-by-step solution:
Step 1: Understand the Given Information
- Mass of the steel ball (m) = 400 g = 0.4 kg (convert grams to kilograms by dividing by 1000)
- Initial velocity (u) = 15 m/s
- Average force (F) = 900 N (acting in the opposite direction)
- Time duration of the collision (Δt) = 30 ms = 30 × 10^(-3) s (convert milliseconds to seconds)
Step 2: Calculate the Initial Momentum
The initial momentum (P_initial) can be calculated using the formula:
Pinitial=m×u
Substituting the values:
Pinitial=0.4kg×15m/s=6kg m/s
Step 3: Use Newton's Second Law to Find Change in Momentum
According to Newton's second law, the change in momentum (ΔP) can be expressed as:
F×Δt=Pfinal−Pinitial
Rearranging gives us:
Pfinal=Pinitial+F×Δt
Step 4: Calculate the Change in Momentum
Now, we can calculate the change in momentum:
F×Δt=900N×30×10−3s=900×0.03=27kg m/s
Step 5: Calculate Final Momentum
Since the force is acting in the opposite direction, we need to subtract the change in momentum from the initial momentum:
Pfinal=Pinitial−(F×Δt)
Substituting the values:
Pfinal=6kg m/s−27kg m/s=−21kg m/s
Step 6: Find the Magnitude of Final Momentum
The magnitude of the final momentum is:
|Pfinal|=21kg m/s
Conclusion
The magnitude of the final momentum of the ball is 21 kg m/s.
---
- Mass of the steel ball (m) = 400 g = 0.4 kg (convert grams to kilograms by dividing by 1000)
- Initial velocity (u) = 15 m/s
- Average force (F) = 900 N (acting in the opposite direction)
- Time duration of the collision (Δt) = 30 ms = 30 × 10^(-3) s (convert milliseconds to seconds)
The initial momentum (P_initial) can be calculated using the formula:
Pinitial=m×u
Substituting the values:
Pinitial=0.4kg×15m/s=6kg m/s
According to Newton's second law, the change in momentum (ΔP) can be expressed as:
F×Δt=Pfinal−Pinitial
Rearranging gives us:
Pfinal=Pinitial+F×Δt
Now, we can calculate the change in momentum:
F×Δt=900N×30×10−3s=900×0.03=27kg m/s
Since the force is acting in the opposite direction, we need to subtract the change in momentum from the initial momentum:
Pfinal=Pinitial−(F×Δt)
Substituting the values:
Pfinal=6kg m/s−27kg m/s=−21kg m/s
The magnitude of the final momentum is:
|Pfinal|=21kg m/s
The magnitude of the final momentum of the ball is 21 kg m/s.
Topper's Solved these Questions
- NSO QUESTION PAPER 2020 SET 1BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - NSO QUESTION PAPER 2020 SET 1EXERCISE - ACHIEVERS SECTION
1 Video
- NSO QUESTION PAPER 2019 SET BBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - NSO QUESTION PAPER 2019 SET BEXERCISE - ACHIEVERS SECTION
1 Video
- NSO QUESTION PAPER 2020 SET 2BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - NSO QUESTION PAPER 2020 SET 2EXERCISE - ACHIEVERS SECTION
1 Video
Similar Questions
2kg ball moving at 6ms−1 collides head on with a 3kg ball moving in the opposite direction at 12m/s .The velocity of each ball after the impact, if the coefficient of restitution is 1/2, is ?
View SolutionA ball of mass 10g is initially moving with a velocity of 50ms−1 On applying a constant force a ball for 2.0s, it acquires a velocity of 70ms−1 calculate
the final momentum of ball
View Solution
Knowledge Check
A force of 1200 N acts on a 0,6 kg steel ball as a result of collision lasting 25 ms. If the force is in a direction opposite to the initial velocity of 14ms1, then the final speed of the steel ball would be
A24ms−1B35ms−1C12ms−1D46ms−1A force of 1200 N acts on a 0.5 kg steel ball as a result of collision lasting 25 ms. If the force is in a direction opposite to the initial velocity of 14 ms, then the final speed of the steel ball would be
A24ms−1B35ms−1C12ms−1D46ms−1A 1kg ball moving at 12m/s collides head on with a 2g ball moving in the opposite direction at 24m/s. The velocity of each ball after the impact, if the coefficient of restitution is 2/3 is
A12m/s,36m/sB−28m/s,−4m/sC20m/s,24m/sD−20m/s,−4m/s
A ball of mass 10g is initially moving with a velocity of 50ms−1 On applying a constant force a ball for 2.0s, it acquires a velocity of 70ms−1 calculate
the initial momentum of ball
View SolutionThe velocity time graph of a ball moving on the surface of a floor is shown in figure. Find the force acting on the ball if the mass of the ball is 50g.
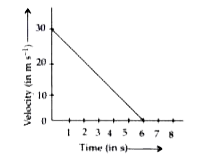
View SolutionThe first ball of mass m moving with a velocity u collides head on with the second ball of mass m at rest. If the coefficient of restitution is e, the ratio of final velocity of the second ball to the initial velocity of the first ball is
View SolutionA ball of mass 0⋅2 kg moving with a speed of 30 m/s strikes a bat returns in opposite direction with speed of 90m/s . Magnitude of change in momentu,m of ball will be
View SolutionConsider a ball fells from a height of 2 m and rebounds to a height of 0.5 m. If the mass of the ball is 60 g, then find the impulse and the average force between the ball and the ground. The time for which the ball and the ground are in contact was 0.2 s. The initial velocity of the ball at P is zero. Let the final velocity of the ball at Q is v.
View Solution

