A brief information about a few substances is given as :
X It is the residue left behind after destructive distillation of coal.
Y : It is a mixture of hydrogen, methane, carbon monoxide and other gases.
Z : It contains several carbon compounds which are used to make pesticides, explosives, synthetic fibres, perfumes, etc.
X, Y and Z are respectively
Kerosene, CNG and ammoniacal liquor
Bitumen, coal gas and coal tar
Coke, coal gas and coal tar
Petrol, CNG and bitumen.
The correct Answer is:C
To solve the question, we need to identify the substances X, Y, and Z based on the descriptions provided.
1. Identify Substance X:
- The question states that X is the residue left behind after the destructive distillation of coal.
- In the process of destructive distillation, coal is heated in the absence of air, leading to the formation of several products.
- The solid residue that remains after this process is known as coke.
Conclusion: X = Coke
2. Identify Substance Y:
- The question describes Y as a mixture of hydrogen, methane, carbon monoxide, and other gases.
- This mixture is produced during the destructive distillation of coal and is commonly referred to as coal gas.
Conclusion: Y = Coal gas
3. Identify Substance Z:
- The description for Z states that it contains several carbon compounds used to make pesticides, explosives, synthetic fibers, perfumes, etc.
- This substance is derived from the tar produced during the destructive distillation of coal, known as coal tar.
Conclusion: Z = Coal tar
4. Final Answer:
- Therefore, the substances X, Y, and Z are:
- X = Coke
- Y = Coal gas
- Z = Coal tar
Final Answer:
X, Y, and Z are respectively Coke, Coal gas, and Coal tar.
---
- The question states that X is the residue left behind after the destructive distillation of coal.
- In the process of destructive distillation, coal is heated in the absence of air, leading to the formation of several products.
- The solid residue that remains after this process is known as coke.
- The question describes Y as a mixture of hydrogen, methane, carbon monoxide, and other gases.
- This mixture is produced during the destructive distillation of coal and is commonly referred to as coal gas.
- The description for Z states that it contains several carbon compounds used to make pesticides, explosives, synthetic fibers, perfumes, etc.
- This substance is derived from the tar produced during the destructive distillation of coal, known as coal tar.
- Therefore, the substances X, Y, and Z are:
- X = Coke
- Y = Coal gas
- Z = Coal tar
X, Y, and Z are respectively Coke, Coal gas, and Coal tar.
Topper's Solved these Questions
Similar Questions
Read the given passage and answer questions number 1 to 5 that follow :
Carbohydrates are primarily produced by plants and form a very large group of naturally occurring organic compounds. Some common examples of carbohydrates are cane sugar, glucose, starch, etc. Most of them have a general formula, Cx(H2O)y and were considered as hydrates of carbon from where the name carbohydrate was derived. For example, the molecular formula of glucose (C6H12O6) fits into this general formula, C6(H2O)2. But all the compounds which fit into this formula may not be classified as carbohydrates. For example, acetic acid (CH3COOH) fits into this general formula, C2(H2O)2 but is not a carbohydrate. Similarly, rhamnose, C6H12O5is a carbohydrate but does not fit in this definition. A large number of their reactions have shown that they contain specific functional groups. Chemically, the carbohydrates may be defined as optically active polyhydroxy aldehydes or ketones or the compounds which produce such units on hydrolysis. Some of the carbohydrates, which are sweet in taste, are also called sugars. The most common sugar, used in our homes is named as sucrose whereas the sugar present in milk is known as lactose. Carbohydrates are also called saccharides.
Give some examples of carbohydrates.
View SolutionRead the given passage and answer questions number 1 to 5 that follow :
Carbohydrates are primarily produced by plants and form a very large group of naturally occurring organic compounds. Some common examples of carbohydrates are cane sugar, glucose, starch, etc. Most of them have a general formula, Cx(H2O)y and were considered as hydrates of carbon from where the name carbohydrate was derived. For example, the molecular formula of glucose (C6H12O6) fits into this general formula, C6(H2O)2. But all the compounds which fit into this formula may not be classified as carbohydrates. For example, acetic acid (CH3COOH) fits into this general formula, C2(H2O)2 but is not a carbohydrate. Similarly, rhamnose, C6H12O5is a carbohydrate but does not fit in this definition. A large number of their reactions have shown that they contain specific functional groups. Chemically, the carbohydrates may be defined as optically active polyhydroxy aldehydes or ketones or the compounds which produce such units on hydrolysis. Some of the carbohydrates, which are sweet in taste, are also called sugars. The most common sugar, used in our homes is named as sucrose whereas the sugar present in milk is known as lactose. Carbohydrates are also called saccharides.
Name the carbohydrate present in milk.
View Solution
Knowledge Check
The constituents of a heterogeneous mixture are X, Y and Z. If mixture containing X and Y is taken, X can be separated using magnetic separation, Y and Z can be separated using distillation method. Which of the following best identifies X, Y and Z respectively?
AIron, salt, waterBSulphur, carbon disulphide, waterCGun powder, common salt, waterDlodine, sand, alcoholRead the paragraph carefully and answer the following questions:
During gas analysis, the eudiometer tube filled with mercury is inverted over a trough containing. mercury. A known volume of the gas. or gaseous mixture to be studied is next introduced, which displaces an equivalent amount of mercury. Next a known amount, of oxygen in excess is introduced and the electric spark is passed, whereby the combustible material gets oxidized. The volume of carbon dioxide, water vapour or other gaseous products of combustíon are next determined by absorbing them in suitable reagents. The various reagents used for absorbing different gases areO3→ turpentine oil
O2→ alkalino pyragallol
CO2,SO2→ alkali solution [NaOH,KOH,Ca(OH)2]
0.2 mole sample of hydrocarbon CxHy yields after complete combustion with excess O2 gas, 0.8 mole of CO2, 1.1 mole of H2O. Hence,, hydrocarbon isAC4H10BC4H8CC4H5DC8H16After the faliure of Bohr atomic theory but its ability to explain to the atomic spectral a need was felt for the new model that could incorporate, the concept of stationary orbit, de Broglie concept, Heisenberg uncertainity principle. The concept that in corporate above facts is called quantum mechanics of the atomic model wave mchanical model. it includes set of quantum number and ∣∣ψ2∣∣ a mathematical expression of the probability of finding an electron at all points in space. This probability function is the best indication available of how the electon behaves, for as a consequence of the Uncertainity Principle, the amount we can know about the electron is limited. While quantum mechanics can tell us the exact probability of finding an electron at any two particular points, it does not tell us how the electron moves from one of these points to the other. Thus the idea of an electron orbit is lost, it is replaced with a description of where the electron is most likely to be found. This total picture of the probability of finding an electron at various points in space is called an orbital.
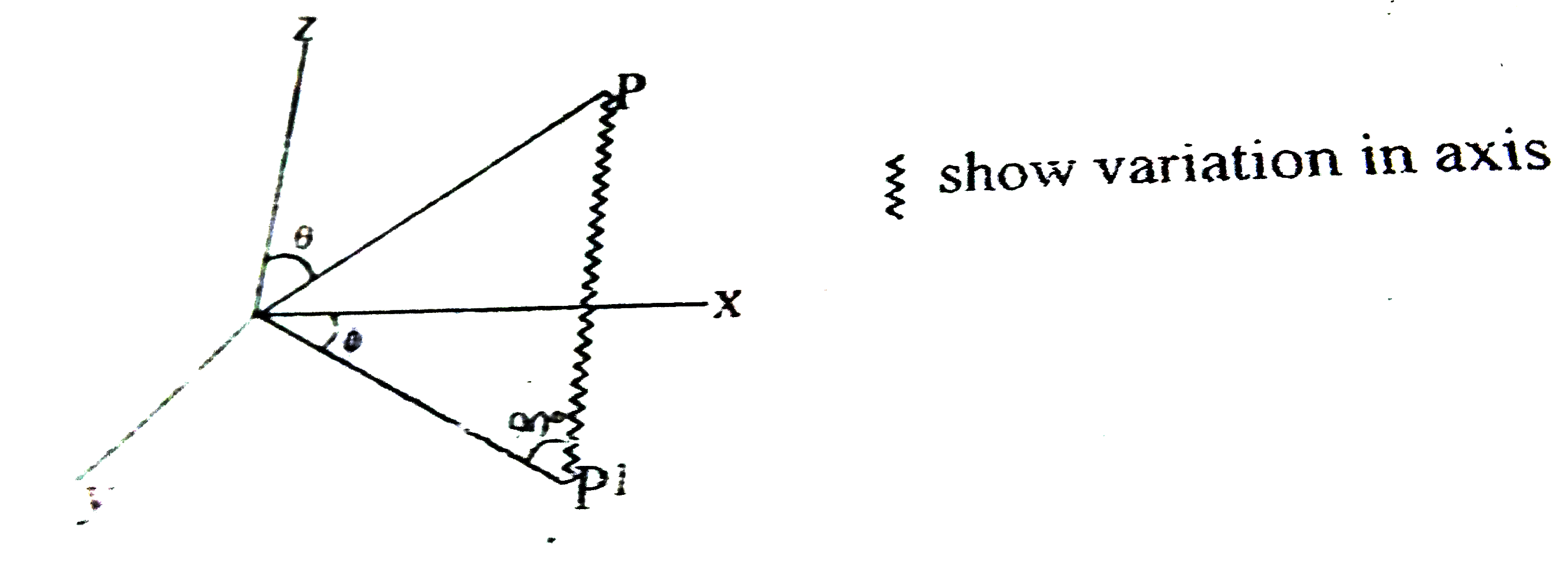
There are various types of orbitals possible, each corresponding to one of the possible combinations of quantum numbers. These orbitals are classified according to the value of n and l associated with them. In order to avoid confusion over the use of two numbers, the numerical velues of l are replaced by letters, electrons in orbitals with l=0 are called s-electrons those occupying orbitals for which l=1 are p-electrons and those for which l=2 are called d-electrons. The numerical and alphabetical correspondences are summarized in table. Using the alphabetical notation for l, we would say that in the ground state of hydrogen atom (n=1,l=0) we have a 1s-electron, or that the electron moves in a 1s-orbital. The relation of the spherical polar co-ordinates r,θ and ϕ to Cartesian coordinates x, y and z. To make the concept of an orbital more meaningful, it is helpful to examine the actual solution of the wave function for the one-electron atom. Because of the spherical sysmmetry of the atom, the wave functions are most simply expressed in terms of a spherical polar-coordinate system, shown in fig., which has its orbit at the nucleus. It is found that the wave function can be expressed as the product of two functions, one of which (the ''angular part'' X) depends only the angle θ and ϕ the other of which (the ''radial part'' R) depends only on the distance from the nucleus. Thus we have
ϕ(r,θ,ϕ)=R(r)X(θ,ϕ)
Angular and radial parts of hydrogen atom wave function
(Angular partX(θ,ϕ),,Radial partRn,l(r)),(X(s)=(14π)1/2,,R(1s)=2(za0)3/2e−σ/2),(X(px)=(34π)1/2sinθcosϕ,,R(2s)=12√2(za0)3/2(2−σ)e−σ/2),(X(py)=(34π)1/2sinθsinϕ,,R(2p)=12√6(za0)3/2σe−σ/2),(X(pz)=(34π)1/2cosθ,,),(X(d22)=(516π)1/2(3cos2θ−1),,),(X(dxz)=(154π)1/2sinθcosθcosϕ,,R(3s)=19√3(za0)3/2(6−6σ+σ2)e−σ/2),(X(dyz)=(154π)1/2sinθcosθsinϕ,,R(3p)=19√6(za0)3/2(4−σ)σe−σ/2),(X(dx2−y2)=(154π)1/2sin2θcos2ϕ,,R(3d)=19√30(za0)3/2σ2e−σ/2),(X(dxy)=(154π)1/2sin2θsin2ϕ,,),(,,σ=2Zrna0,a0=h24π2me2)
This factrorization helps us to visualize the wave function, since it allows us to consider the angular and radial dependences separately. It contains the expression for the angular and radial parts of the one electron atom wave function. Note that the angular part of the wave function for an s-orbital it alwats the same, (1/4π)1/2 regardless of principal quantum number. It is also true that the angular dependence of the p-orbitals and of the d-orbitals is independent of principle quantum number. Thus all orbitals of given types (s, p, or d) have the same angular behavour The table shows, however, that the radial part of the wave function depends both on the principal quantum n and on the angular momentum quantum number l.
To find the wave function for a particular state, we simply multiply the appropriate angular and radial parts togather called normalized wave function.
The probability of finding an electron at a point within an atom is proportional to the square of orbital wave function, i.e., ψ2 at that point. Thus, ψ2 is known as probability density and always a positive quantity.
ψ2dV(orψ2.4πr2dr). represents the probability for finding electron in a small volume dV surrounding the nucleus.
The angular wave function of which orbital with not disturb by the variation with azimuthal angle onlyA1s and 2sB2pz and 2d2zC2px and 3d2zD2px and 2s
Read the given passage and answer questions number 1 to 5 that follow :
Carbohydrates are primarily produced by plants and form a very large group of naturally occurring organic compounds. Some common examples of carbohydrates are cane sugar, glucose, starch, etc. Most of them have a general formula, Cx(H2O)y and were considered as hydrates of carbon from where the name carbohydrate was derived. For example, the molecular formula of glucose (C6H12O6) fits into this general formula, C6(H2O)2. But all the compounds which fit into this formula may not be classified as carbohydrates. For example, acetic acid (CH3COOH) fits into this general formula, C2(H2O)2 but is not a carbohydrate. Similarly, rhamnose, C6H12O5is a carbohydrate but does not fit in this definition. A large number of their reactions have shown that they contain specific functional groups. Chemically, the carbohydrates may be defined as optically active polyhydroxy aldehydes or ketones or the compounds which produce such units on hydrolysis. Some of the carbohydrates, which are sweet in taste, are also called sugars. The most common sugar, used in our homes is named as sucrose whereas the sugar present in milk is known as lactose. Carbohydrates are also called saccharides.
Write the molecular formula for cane sugar.
View SolutionRead the given passage and answer questions number 1 to 5 that follow :
Carbohydrates are primarily produced by plants and form a very large group of naturally occurring organic compounds. Some common examples of carbohydrates are cane sugar, glucose, starch, etc. Most of them have a general formula, Cx(H2O)y and were considered as hydrates of carbon from where the name carbohydrate was derived. For example, the molecular formula of glucose (C6H12O6) fits into this general formula, C6(H2O)2. But all the compounds which fit into this formula may not be classified as carbohydrates. For example, acetic acid (CH3COOH) fits into this general formula, C2(H2O)2 but is not a carbohydrate. Similarly, rhamnose, C6H12O5is a carbohydrate but does not fit in this definition. A large number of their reactions have shown that they contain specific functional groups. Chemically, the carbohydrates may be defined as optically active polyhydroxy aldehydes or ketones or the compounds which produce such units on hydrolysis. Some of the carbohydrates, which are sweet in taste, are also called sugars. The most common sugar, used in our homes is named as sucrose whereas the sugar present in milk is known as lactose. Carbohydrates are also called saccharides.
Most of the carbohydrates fit into a general formula. What is that?
View SolutionRead the given passage and answer questions number 1 to 5 that follow :
Carbohydrates are primarily produced by plants and form a very large group of naturally occurring organic compounds. Some common examples of carbohydrates are cane sugar, glucose, starch, etc. Most of them have a general formula, Cx(H2O)y and were considered as hydrates of carbon from where the name carbohydrate was derived. For example, the molecular formula of glucose (C6H12O6) fits into this general formula, C6(H2O)2. But all the compounds which fit into this formula may not be classified as carbohydrates. For example, acetic acid (CH3COOH) fits into this general formula, C2(H2O)2 but is not a carbohydrate. Similarly, rhamnose, C6H12O5is a carbohydrate but does not fit in this definition. A large number of their reactions have shown that they contain specific functional groups. Chemically, the carbohydrates may be defined as optically active polyhydroxy aldehydes or ketones or the compounds which produce such units on hydrolysis. Some of the carbohydrates, which are sweet in taste, are also called sugars. The most common sugar, used in our homes is named as sucrose whereas the sugar present in milk is known as lactose. Carbohydrates are also called saccharides.
How do you define a carbohydrate chemically ?
View SolutionA metal carbonate X on reacting with an acid gives a gas which when passed through a solution Y gives the carbonate back. On the other hand, a gas G that is obtained at anode during electrolysis of brine is passed on dry Y, it gives a compound Z, used for disinfecting drinking water . Identify X,Y,G and Z.
View SolutionAfter the faliure of Bohr atomic theory but its ability to explain to the atomic spectral a need was felt for the new model that could incorporate, the concept of stationary orbit, de Broglie concept, Heisenberg uncertainity principle. The concept that in corporate above facts is called quantum mechanics of the atomic model wave mchanical model. it includes set of quantum number and ∣∣ψ2∣∣ a mathematical expression of the probability of finding an electron at all points in space. This probability function is the best indication available of how the electon behaves, for as a consequence of the Uncertainity Principle, the amount we can know about the electron is limited. While quantum mechanics can tell us the exact probability of finding an electron at any two particular points, it does not tell us how the electron moves from one of these points to the other. Thus the idea of an electron orbit is lost, it is replaced with a description of where the electron is most likely to be found. This total picture of the probability of finding an electron at various points in space is called an orbital.
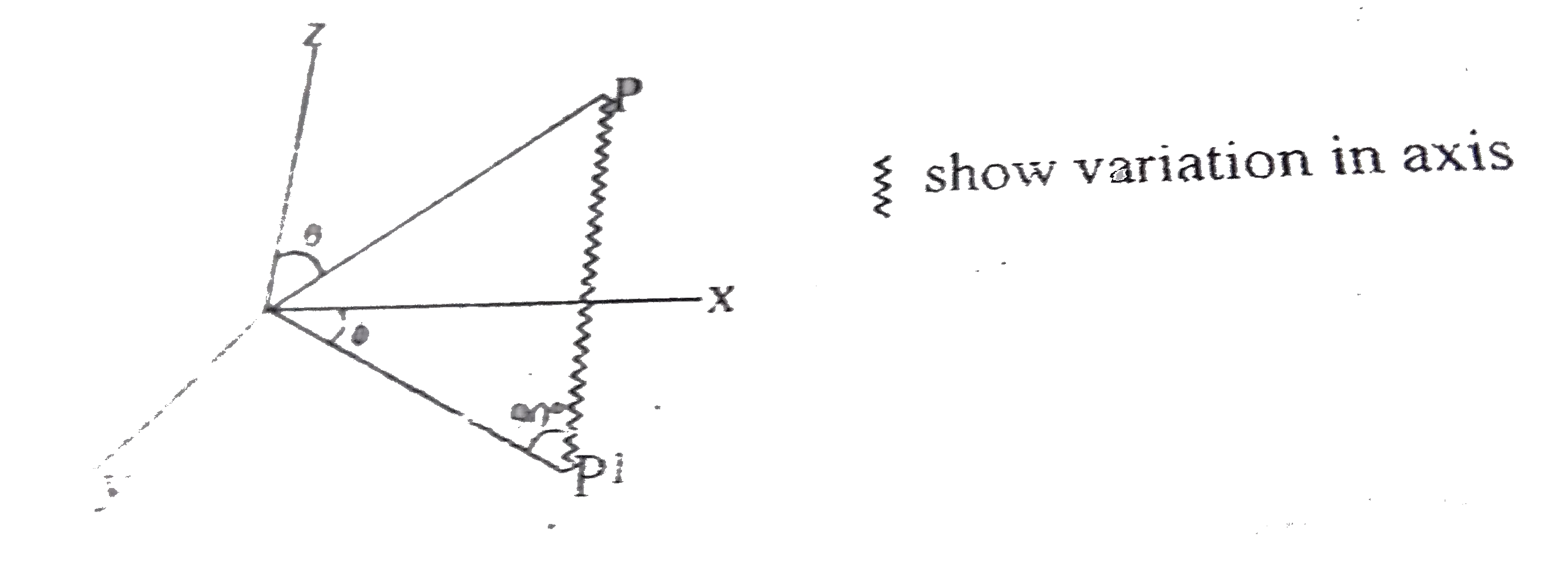
There are various types of orbitals possible, each corresponding to one of the possible combinations of quantum numbers. These orbitals are classified according to the value of n and l associated with them. In order to avoid confusion over the use of two numbers, the numerical velues of l are replaced by letters, electrons in orbitals with l=0 are called s-electrons those occupying orbitals for which l=1 are p-electrons and those for which l=2 are called d-electrons. The numerical and alphabetical correspondences are summarized in table. Using the alphabetical notation for l, we would say that in the ground state of hydrogen atom (n=1,l=0) we have a 1s-electron, or that the electron moves in a 1s-orbital. The relation of the spherical polar co-ordinates r,θ and ϕ to Cartesian coordinates x, y and z. To make the concept of an orbital more meaningful, it is helpful to examine the actual solution of the wave function for the one-electron atom. Because of the spherical sysmmetry of the atom, the wave functions are most simply expressed in terms of a spherical polar-coordinate system, shown in fig., which has its orbit at the nucleus. It is found that the wave function can be expressed as the product of two functions, one of which (the ''angular part'' X) depends only the angle θ and ϕ the other of which (the ''radial part'' R) depends only on the distance from the nucleus. Thus we have
ϕ(r,θ,ϕ)=R(r)X(θ,ϕ)
Angular and radial parts of hydrogen atom wave function
(Angular partX(θ,ϕ),,Radial partRn,l(r)),(X(s)=(14π)1/2,,R(1s)=2(za0)3/2e−σ/2),(X(px)=(34π)1/2sinθcosϕ,,R(2s)=12√2(za0)3/2(2−σ)e−σ/2),(X(py)=(34π)1/2sinθsinϕ,,R(2p)=12√6(za0)3/2σe−σ/2),(X(pz)=(34π)1/2cosθ,,),(X(d22)=(516π)1/2(3cos2θ−1),,),(X(dxz)=(154π)1/2sinθcosθcosϕ,,R(3s)=19√3(za0)3/2(6−6σ+σ2)e−σ/2),(X(dyz)=(154π)1/2sinθcosθsinϕ,,R(3p)=19√6(za0)3/2(4−σ)σe−σ/2),(X(dx2−y2)=(154π)1/2sin2θcos2ϕ,,R(3d)=19√30(za0)3/2σ2e−σ/2),(X(dxy)=(154π)1/2sin2θsin2ϕ,,),(,,σ=2Zrna0,a0=h24π2me2)
This factrorization helps us to visualize the wave function, since it allows us to consider the angular and radial dependences separately. It contains the expression for the angular and radial parts of the one electron atom wave function. Note that the angular part of the wave function for an s-orbital it alwats the same, (1/4π)1/2 regardless of principal quantum number. It is also true that the angular dependence of the p-orbitals and of the d-orbitals is independent of principle quantum number. Thus all orbitals of given types (s, p, or d) have the same angular behavour The table shows, however, that the radial part of the wave function depends both on the principal quantum n and on the angular momentum quantum number l.
To find the wave function for a particular state, we simply multiply the appropriate angular and radial parts togather called normalized wave function.
The probability of finding an electron at a point within an atom is proportional to the square of orbital wave function, i.e., ψ2 at that point. Thus, ψ2 is known as probability density and always a positive quantity.
ψ2dV(orψ2.4πr2dr). represents the probability for finding electron in a small volume dV surrounding the nucleus.
The electron probility density for 1s-orbital best represented by the relation.
View Solution
