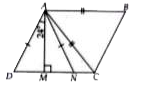
If ABCD is a parallelogram, ΔADNandΔABC are isosceles triangles, then find ∠BAC.
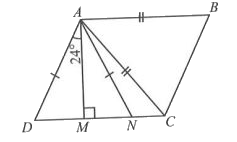
112∘
140∘
48∘
32∘
The correct Answer is:C
Step by step video, text & image solution for If ABCD is a parallelogram, Delta ADN and Delta ABC are isosceles triangles, then find angleBAC. by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Updated on:21/07/2023Topper's Solved these Questions
- IMO QUESTION PAPER 2018-19 SET- ABOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2018-19 SET- AEXERCISE - Everyday Mathematics
10 Videos
- IMO QUESTION PAPER 2018-19 SET- ABOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2018-19 SET- AEXERCISE - Achievers Section
5 Videos
- IMO QUESTION PAPER 2018-19 SET -B BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2018-19 SET -B EXERCISE - ACHIEVERS SECTION
5 Videos
- IMO QUESTION PAPER 2019-20 SET ABOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2019-20 SET AEXERCISE - Achievers Section
5 Videos
Similar Questions
Knowledge Check
The area of a parallelogram ABCD is equal to that right angled isosceles triangle whose hypotenuse is l cm. If O is a point inside the parallelogram ABCD then sum of areas of ΔAOBandΔCOD is.
Al22cm2Bl24cm2Cl28cm2Dl216cm2In an isosceles triangle ABC, AB=AC and ∠A=3∠B. Find ∠C.
A36∘B32∘C28∘D40∘
In the given figure (not to scale), ABC is an isosceles triangle in which AB=AC. AEDC is a parallelogram. If ∠CDF=70∘ and ∠BFE=180∘, then find ∠FBA.
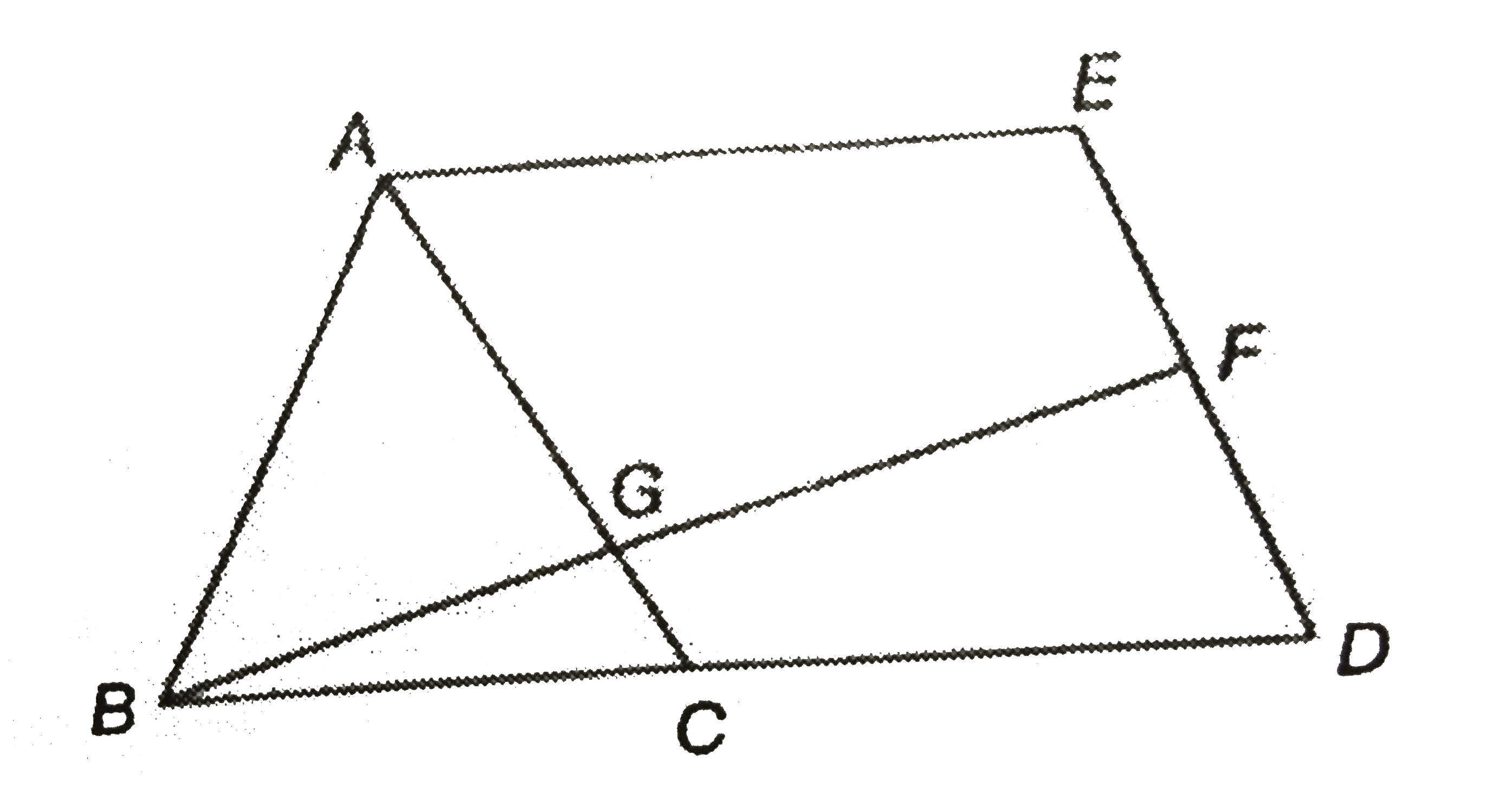
View SolutionFind the ratio of area of ΔADE to Δ ABC

View SolutionIn the given figure, ABCD is a parallelogram. Find the area of ΔAED

View SolutionIn the adjoining figure, ΔABC is an isosceles triangle. Find the value of ∠BDC and ∠BEC.
View SolutionIn the adjoning figure, ABCD is a parallelogram. Prove that : area of ΔBPC= area of ΔDPQ

View SolutionIn the figure given below, ABC is a triangle with AB = BC and D is an interior point of the triangle ABC such that ∠DAC=∠DCA.

Consider the following statements :
1. Triangle ADC is an isosceles triangle.
2. Dis the centroid of the triangle ABC.
3. Triangle ABD is congruent to the triangle CBD.
Which of the above statements are correct ?
View Solution