Question

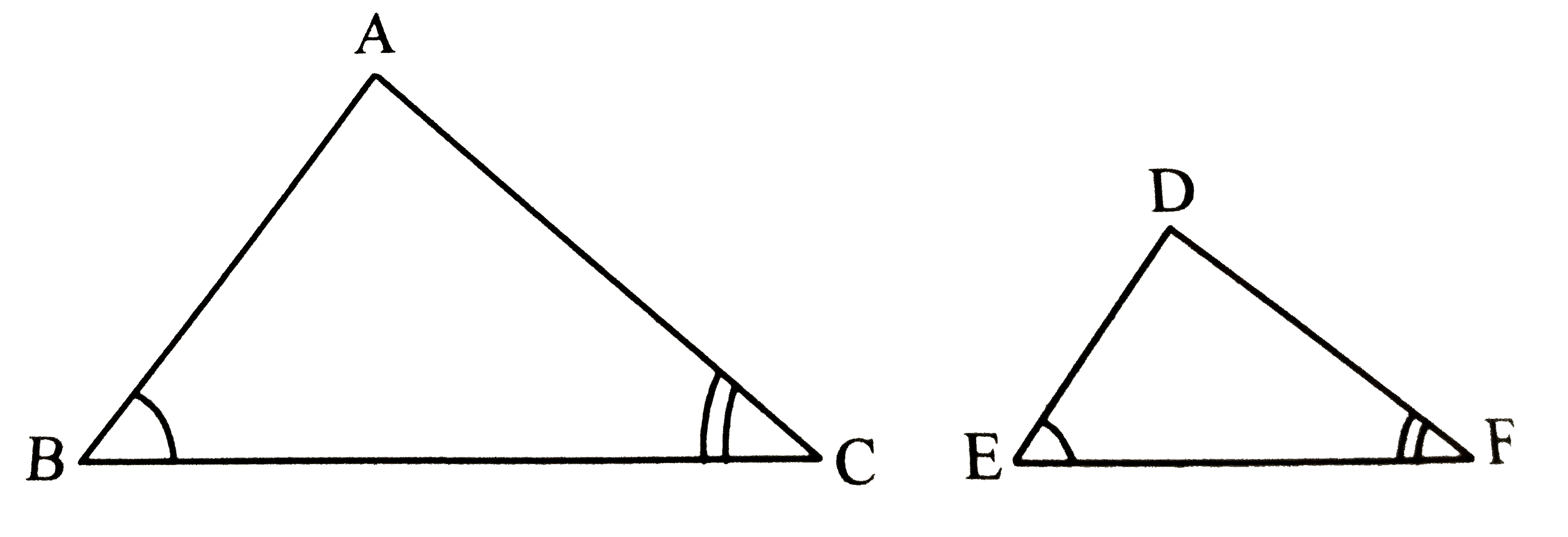
In two triangle ABC and DEF, if AB = BC , $\angle B=\angle E$, DE=EF and BC = Ef , then which of the following statements is CORRECT ?

Options

A. Triangles are congruent only .
B. Triangles are isosceles only .
C. Both triangles are congruent and isosceles
D. Both the triangles are neither congruent nor isosceles .

Answer

C

Explanation

To solve the problem, we need to analyze the given information about triangles ABC and DEF step by step.

Step 1: Understand the Given Information
We are given:
- AB = BC (Two sides of triangle ABC are equal)
- ∠B = ∠E (Angle B in triangle ABC is equal to angle E in triangle DEF)
- DE = EF (Two sides of triangle DEF are equal)
- BC = EF (The side BC in triangle ABC is equal to the side EF in triangle DEF)

Step 2: Identify the Type of Triangles
Since AB = BC, triangle ABC is an isosceles triangle. Similarly, since DE = EF, triangle DEF is also an isosceles triangle.

Step 3: Analyze the Angles
We know that in triangle ABC:
- AB = BC implies that ∠A = ∠C (the angles opposite to the equal sides are equal).

In triangle DEF:
- DE = EF implies that ∠D = ∠F (the angles opposite to the equal sides are equal).

Step 4: Compare the Triangles
Now we have:
- ∠B = ∠E (given)
- ∠A = ∠C (from triangle ABC)
- ∠D = ∠F (from triangle DEF)

Step 5: Use the SAS Congruence Criterion
We can now apply the SAS (Side-Angle-Side) congruence criterion:
- AB = EF (given)
- ∠B = ∠E (given)
- BC = DE (since BC = EF and DE = EF, we can say BC = DE)

Thus, we have two sides and the included angle equal in both triangles:
- AB = EF
- ∠B = ∠E
- BC = DE

Conclusion
By the SAS criterion, triangle ABC is congruent to triangle DEF. Therefore, the correct statement is that both triangles are congruent and isosceles.