A cuboidal metal of dimensions 44cm×30cm×15 cm was melted and cast into a cylinder of height 28 cm. Its radius is_____.
20 cm
15 cm
10 cm
25 cm
The correct Answer is:B
To find the radius of the cylinder formed by melting a cuboidal metal, we will follow these steps:
Step 1: Calculate the volume of the cuboid.
The volume V of a cuboid is given by the formula:
V=length×breadth×height
Substituting the given dimensions:
V=44cm×30cm×15cm
Step 2: Perform the multiplication.
Calculating the volume:
V=44×30=1320cm2
Now, multiply this result by the height:
V=1320×15=19800cm3
Step 3: Set the volume of the cylinder equal to the volume of the cuboid.
The volume V of a cylinder is given by the formula:
V=πr2h
where r is the radius and h is the height of the cylinder. We know the height of the cylinder is 28 cm:
19800=πr2×28
Step 4: Substitute the value of π.
Using π≈227:
19800=227r2×28
Step 5: Simplify the equation.
Rearranging gives:
19800=22×287r2
Calculating 22×287:
22×287=6167=88
So, we have:
19800=88r2
Step 6: Solve for r2.
Dividing both sides by 88:
r2=1980088
Step 7: Perform the division.
Calculating:
r2=225
Step 8: Find the radius r.
Taking the square root of both sides:
r=√225=15cm
Thus, the radius of the cylinder is 15 cm.
---
The volume V of a cuboid is given by the formula:
V=length×breadth×height
Substituting the given dimensions:
V=44cm×30cm×15cm
Calculating the volume:
V=44×30=1320cm2
Now, multiply this result by the height:
V=1320×15=19800cm3
The volume V of a cylinder is given by the formula:
V=πr2h
where r is the radius and h is the height of the cylinder. We know the height of the cylinder is 28 cm:
19800=πr2×28
Using π≈227:
19800=227r2×28
Rearranging gives:
19800=22×287r2
Calculating 22×287:
22×287=6167=88
So, we have:
19800=88r2
Dividing both sides by 88:
r2=1980088
Calculating:
r2=225
Taking the square root of both sides:
r=√225=15cm
Topper's Solved these Questions
- SURFACE AREAS AND VOLUMES BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - SURFACE AREAS AND VOLUMES EXERCISE - Everday Mathematics
4 Videos
- SURFACE AREAS AND VOLUMES BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - SURFACE AREAS AND VOLUMES EXERCISE - Achievers section (Hots)
3 Videos
- STATISTICS BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - STATISTICS EXERCISE - Achievers section (Hots)
3 Videos
- TRIANGLESBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - TRIANGLESEXERCISE - ACHIEVERS SECTION (HOTS)
5 Videos
Similar Questions
A metal cuboid of dimension 22cm×15cm×7.5cm was melted and casted into a cylinder of height 14 cm Find its radius
View SolutionA solid metallic cuboid of dimension 24 cm ×11cm×7 cm is melted and recast into solid cones of base radius 3.5 cm and height 6 cm. Find the number of cones so formed.
View Solution
Knowledge Check
A solid sphere of radius 3 cm is melted and recast into a cylinder of radius 2cm. The height of the cylinder is :
A8 cmB9 cmC7 cmD10 cmA solid sphere of radius 3 cm is melted and recast into a cylinder of radius 2 cm. The height of the cylinder is :
A8 cmB9 cmC7 cmD10 cmAssertion (A) : A solid iron in the form of a cuboid of dimensions 49cm×33cm×24cm is melted to form a solid sphere. Then the radius of sphere will be 21 cm.
Reason (R) : Volume of cylinder =πr2h,r is the radius of the cylinder and h is the height of the cylinder.ABoth A and R are true and R is the correct explanation of A.BBoth A and R are true and R is not the correct explanation of A.CA is true but R is falseDA is false but R is true
A solid metallic block of dimensions 4cm×6cm×8cm is melted and recast into solid cubical blocks of edge 2 cm each. The number of recasted cubical blocks will be .....................
View SolutionA solid cuboid with dimensions 18 cm × 12 cm × 8 cm is melted and turned into a cube. What is the length of its edge ?
View SolutionThe dimensions fo a cuboid are 44 cm, 21 cm, 12 cm. It is melted and a cone of height 24 cm is made. Find the radius of its base.
View SolutionThe dimensions of a cuboid are 44 cm, 21 cm, 12 cm. It is melted and a cone of height 24 cm is made. Find the radius of its base.
View SolutionIn the given figure from a cuboidal solid metallic block of dimensions 15cm×10cm×5cm a cylindrical hole of diamter 7 cm is drilled out . Find the suface area of the remaining block .
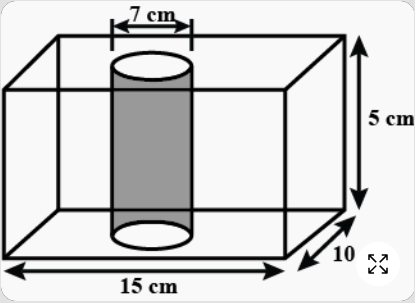
View Solution
