The angles of elevation of an artificial satellite measured from two earth stations are 30∘and60∘ respectively. If the distance between the earth stations, which are in straight line with the point directly below the satellite, is 4000 km, then the height of the satellite is ______ - (Use √3=1.732)
2000 km
6000 km
3464 km
2828 km
The correct Answer is:C
To find the height of the satellite, we will use the information given about the angles of elevation and the distance between the two earth stations.
1. Identify the problem setup:
- Let the height of the satellite be h.
- Let the distance between the two earth stations (point C and D) be 4000 km.
- The angles of elevation from the two stations are 30∘ and 60∘.
2. Draw the diagram:
- Draw a vertical line representing the height h of the satellite.
- Label the point directly below the satellite on the ground as point B.
- Label the two earth stations as point C (where the angle of elevation is 60∘) and point D (where the angle of elevation is 30∘).
- The distance between points C and D is CD=4000 km.
3. Set up the triangles:
- Triangle ABD (where angle DAB=30∘):
- From the definition of tangent, we have:
tan(30∘)=ABDB
Here, AB=h and DB=4000+x (where x is the distance from point B to point C).
- Triangle ABC (where angle CAB=60∘):
- Similarly, we have:
tan(60∘)=ABCB
Here, CB=x.
4. Calculate the tangents:
- We know:
tan(30∘)=1√3andtan(60∘)=√3
- For triangle ABD:
1√3=h4000+x⟹h=4000+x√3
- For triangle ABC:
√3=hx⟹h=x√3
5. Equate the two expressions for h:
- Set the two expressions for h equal to each other:
4000+x√3=x√3
6. Clear the fraction:
- Multiply both sides by √3:
4000+x=3x
- Rearranging gives:
4000=3x−x⟹4000=2x⟹x=2000
7. Substitute back to find h:
- Substitute x=2000 back into the equation for h:
h=2000√3
- Using √3≈1.732:
h=2000×1.732=3464 km
Final Answer:
The height of the satellite is approximately 3464 km.
- Let the height of the satellite be h.
- Let the distance between the two earth stations (point C and D) be 4000 km.
- The angles of elevation from the two stations are 30∘ and 60∘.
- Draw a vertical line representing the height h of the satellite.
- Label the point directly below the satellite on the ground as point B.
- Label the two earth stations as point C (where the angle of elevation is 60∘) and point D (where the angle of elevation is 30∘).
- The distance between points C and D is CD=4000 km.
- Triangle ABD (where angle DAB=30∘):
- From the definition of tangent, we have:
tan(30∘)=ABDB
Here, AB=h and DB=4000+x (where x is the distance from point B to point C).
- Similarly, we have:
tan(60∘)=ABCB
Here, CB=x.
- We know:
tan(30∘)=1√3andtan(60∘)=√3
- For triangle ABD:
1√3=h4000+x⟹h=4000+x√3
- For triangle ABC:
√3=hx⟹h=x√3
- Set the two expressions for h equal to each other:
4000+x√3=x√3
- Multiply both sides by √3:
4000+x=3x
- Rearranging gives:
4000=3x−x⟹4000=2x⟹x=2000
- Substitute x=2000 back into the equation for h:
h=2000√3
- Using √3≈1.732:
h=2000×1.732=3464 km
The height of the satellite is approximately 3464 km.
Topper's Solved these Questions
- SOME APPLICATIONS OF TRIGONOMETRY BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - SOME APPLICATIONS OF TRIGONOMETRY EXERCISE - EVERYDAY MATHEMATICS
4 Videos
- SOME APPLICATIONS OF TRIGONOMETRY BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - SOME APPLICATIONS OF TRIGONOMETRY EXERCISE - ACHIEVERS SECTION (HOTS)
5 Videos
- SOF INTERNATIONAL MATHEMATICS OLYMPIAD QUESTION PAPER 2020BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - SOF INTERNATIONAL MATHEMATICS OLYMPIAD QUESTION PAPER 2020EXERCISE - LOGICAL REASONING
1 Video
- STATISTICS BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - STATISTICS EXERCISE - Achievers section (Hots)
3 Videos
Similar Questions
The angles of elevation of an aeroplane from two places 10 km apart are found to be 60∘and30∘ respectively. Find the height of the aeroplane.
View SolutionThe angles of elevation of the top of an inaccessible tower from two points on the same straight line from the base of the tower are 30° and 60° respectively. If the points are separated at a distance of 100 m, then the height of the tower is close to :
View Solution
Knowledge Check
The angles of elevation of e top of an inaccessible tower from two points on the same straight line from the base of the tower are 30∘and60∘, respectively. If the points are separated at a distance of 100 m, then the height of the tower is close to
A86.5mB80.6mC82.6mD80.6mThe angles of elevation of top and bottom of a flag kept on a flagpost from 30 metres distance are 45∘and30∘ respectively .Height of the flat is (taking √3=1.732)
A12√3 metreB15 metreC14 .32 metreD12. 68 metreTwo satellites are at distances of 2R and 4R respectively from the surface of earth. The ratio of their time periods will be :
A√12527B√27125C√54125D√8125
A Satellite flying at height h is watching the top of the two tallest mountains in Uttarakhand and Karnataka ,them being Nanda Devi(height 7,816m) and Mullayanagiri (height 1,930 m). The angles of depression from the satellite , to the top of Nanda Devi and Mullayanagiri are 30∘and 60∘respectively. If the distance between the peaks of two mountains is 1937 km , and the satellite is vertically above the midpoint of the distance between the two mountains.
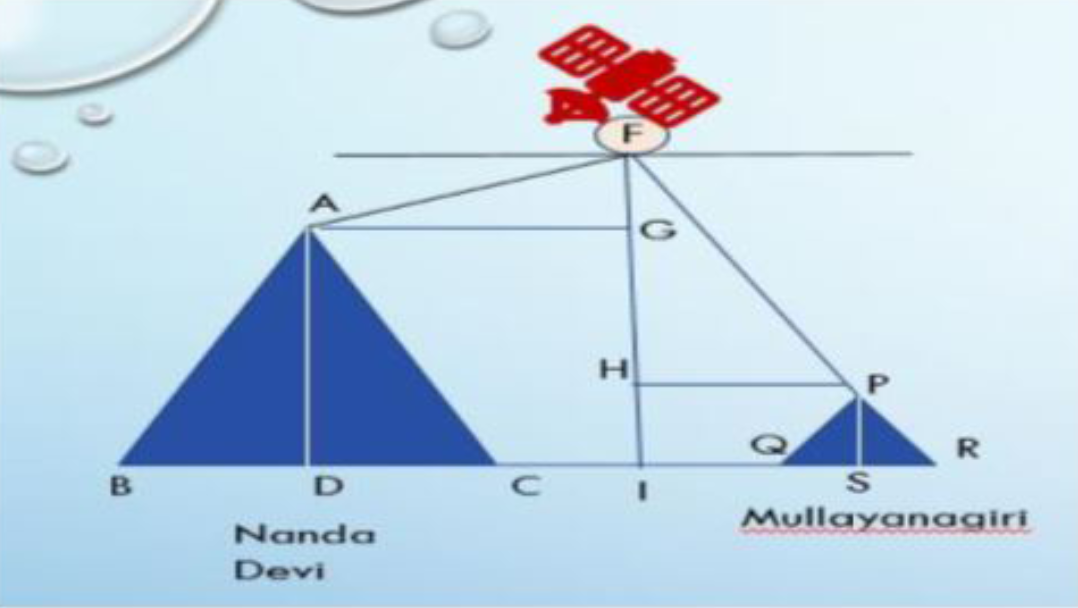
What is the angle of elevation if a man is standing at a distance of 7816m from Nanda Devi?
View SolutionA Satellite flying at height h is watching the top of the two tallest mountains in Uttarakhand and Karnataka ,them being Nanda Devi(height 7,816m) and Mullayanagiri (height 1,930 m). The angles of depression from the satellite , to the top of Nanda Devi and Mullayanagiri are 30∘and 60∘respectively. If the distance between the peaks of two mountains is 1937 km , and the satellite is vertically above the midpoint of the distance between the two mountains.

The distance of the satellite from the top of Nanda Devi is
View SolutionA Satellite flying at height h is watching the top of the two tallest mountains in Uttarakhand and Karnataka ,them being Nanda Devi(height 7,816m) and Mullayanagiri (height 1,930 m). The angles of depression from the satellite , to the top of Nanda Devi and Mullayanagiri are 30∘and 60∘respectively. If the distance between the peaks of two mountains is 1937 km , and the satellite is vertically above the midpoint of the distance between the two mountains.

The distance of the satellite from the ground is
View SolutionA Satellite flying at height h is watching the top of the two tallest mountains in Uttarakhand and Karnataka ,them being Nanda Devi(height 7,816m) and Mullayanagiri (height 1,930 m). The angles of depression from the satellite , to the top of Nanda Devi and Mullayanagiri are 30∘and 60∘respectively. If the distance between the peaks of two mountains is 1937 km , and the satellite is vertically above the midpoint of the distance between the two mountains.

The distance of the satellite from the top of Mullayanagiri is
View SolutionA Satellite flying at height h is watching the top of the two tallest mountains in Uttarakhand and Karnataka ,them being Nanda Devi(height 7,816m) and Mullayanagiri (height 1,930 m). The angles of depression from the satellite , to the top of Nanda Devi and Mullayanagiri are 30∘and 60∘respectively. If the distance between the peaks of two mountains is 1937 km , and the satellite is vertically above the midpoint of the distance between the two mountains.

If a mile stone very far away from, makes 45 to the top of Mullanyangiri montain .So, find the distance of this mile stone form the mountain.
View Solution