If AB=DE,AC=DF,∠A=∠D=90∘ and BC = 5 cm, then EF is equal to _________.
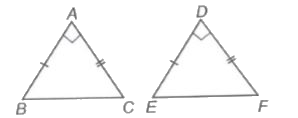
5 cm
4.5 cm
5.5 cm
Can't be determined
The correct Answer is:A
Step by step video & image solution for If AB = DE, AC = DF, angle A = angle D = 90^(@) and BC = 5 cm, then EF is equal to _________. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBook:SCIENCE OLYMPIAD FOUNDATION Chapter:TRIANGLESExercise:Achievers Section (HOTS) (Fill in the blanks.)
Explore 1 Video
- TRIANGLESBook:SCIENCE OLYMPIAD FOUNDATION Chapter:TRIANGLESExercise:Achievers Section (HOTS)
Explore 2 Videos
- SURFACE AREAS AND VOLUMESBook:SCIENCE OLYMPIAD FOUNDATION Chapter:SURFACE AREAS AND VOLUMESExercise:Achievers Section (HOTS)
Explore 3 Videos
Similar Questions
Knowledge Check
If △ABC is an isosceles triangle with ∠c=90∘ and AC = 5 cm then AB is:
A5 cmB2.5 cmC10 cmD5√2cmΔABCandΔDEFare similar. Also ∠A=∠Dand∠B=∠E. If 4AB=DEand BC=12cm, then EF is equal to
A3 cmB24 cmC16 cmD48 cmIn two triangles ABC and FDE, ∠B=∠D=90∘, AC = FE and BC = DE. Then ∠F = ____.
A∠CB∠AC∠BDcan't be determined
In a ΔABC,∠B=90∘andAC=8√2. If AB=BC, then find AB.
View SolutionIn the figure , AC =12 cm ,
∠ABC=90∘, ∠BAC=30∘ ,
then find AB and BC.
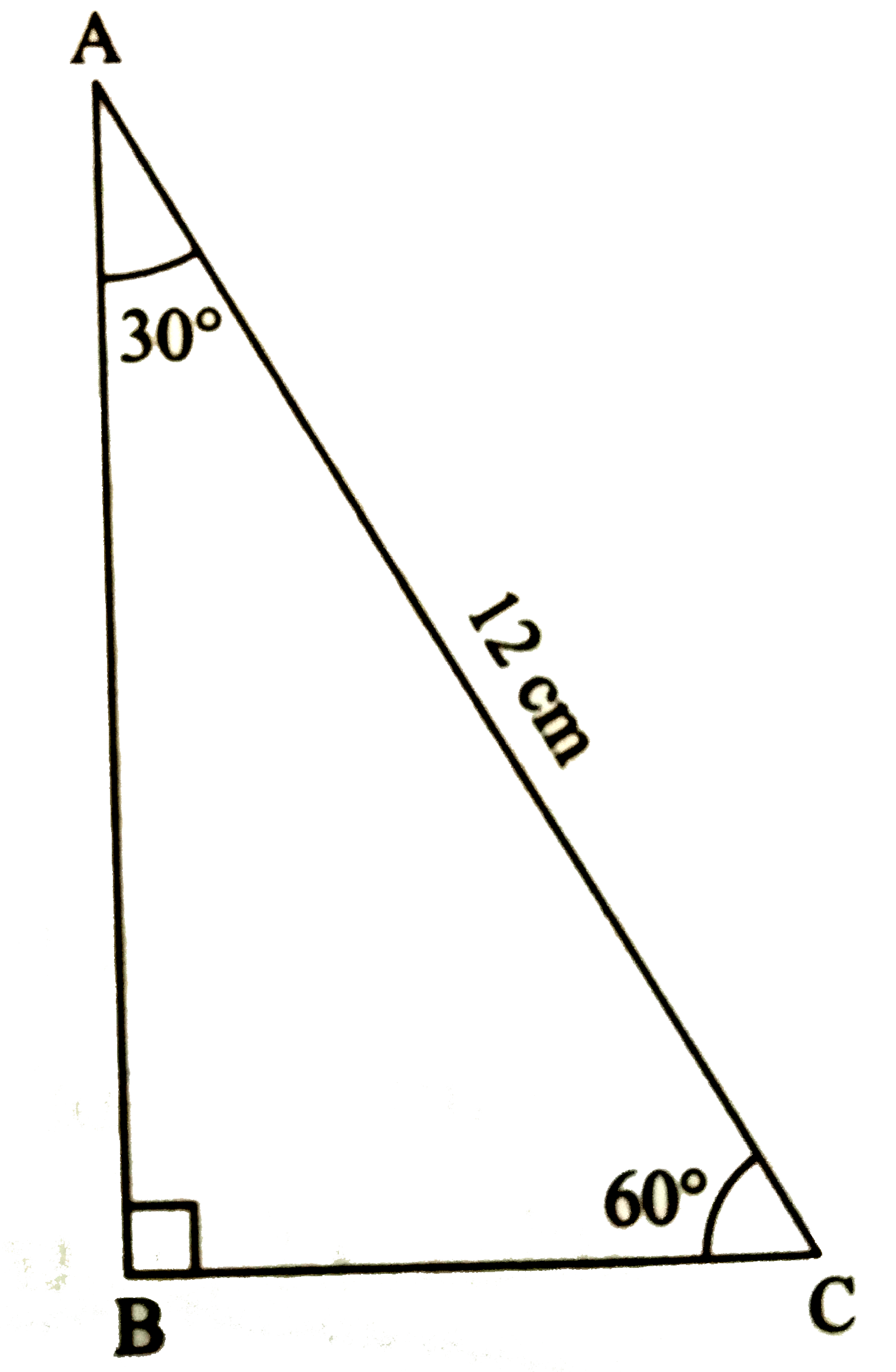
View SolutionIn figure, ABC is a triangle with ∠B=90∘, BC = 3cm and AB = 4cm. D is a point on AC such that AD = 1cm and E is the mid- point of AB. Join D and E and extend DE to meet CB extended at F. Then BF is equal to
View SolutionIf in △ABC, D and E are the points on sides AC and BC, respectively such that DE || AB. F is the point on CE such that DF ||AE. If CE= 6cm and CF = 2.5 cm, then BC is equal to:
त्रिभुज ABC में, D और E क्रमशः भुजाओं AC तथा BC के मध्य बिंदु हैं जो इस प्रकार ह कि DE || AB है F, CE पर स्थित ऐसा बिंदु है कि DF|| AE है | यदि CE= 6 सेमी और CF =2.5 सेमी है, तो BC किसके बराबर है ?
View Solution△ABC is right-angled at A. If AB = 24 cm and AC = 7 cm, then BC = ?
View Solution
