V1,V2,V3 and V4 are the volumes of four cubes of side lengths x cm, 2x cm, 3x cm and 4x cm respectively. Some statements regarding these volumes are shown here
(1) V1+V2+2V3<V4
(2) V1+4V2+V3<V4
(3) 2(V1+V3)+V2=V4
Which of the given statements is CORRECT ?
(1) and (2) only
(2) and (3) only
(1) and (3) only
(1), (2) and (3)
The correct Answer is:D
To solve the problem, we need to calculate the volumes of the cubes based on the given side lengths and then evaluate the three statements provided.
Step 1: Calculate the volumes of the cubes
1. Volume of the first cube (V1):
V1=(xcm)3=x3cm3
2. Volume of the second cube (V2):
V2=(2xcm)3=(23)(x3)=8x3cm3
3. Volume of the third cube (V3):
V3=(3xcm)3=(33)(x3)=27x3cm3
4. Volume of the fourth cube (V4):
V4=(4xcm)3=(43)(x3)=64x3cm3
Step 2: Evaluate the statements
Statement 1: V1+V2+2V3<V4
- Calculate V1+V2+2V3:
V1+V2+2V3=x3+8x3+2(27x3)=x3+8x3+54x3=63x3
- Compare with V4:
63x3<64x3(True)
Statement 2: V1+4V2+V3<V4
- Calculate V1+4V2+V3:
V1+4V2+V3=x3+4(8x3)+27x3=x3+32x3+27x3=60x3
- Compare with V4:
60x3<64x3(True)
Statement 3: 2(V1+V3)+V2=V4
- Calculate 2(V1+V3)+V2:
2(V1+V3)+V2=2(x3+27x3)+8x3=2(28x3)+8x3=56x3+8x3=64x3
- Compare with V4:
64x3=64x3(True)
Conclusion
All three statements are correct.
Final Answer
All statements (1, 2, and 3) are correct.
---
V1=(xcm)3=x3cm3
V2=(2xcm)3=(23)(x3)=8x3cm3
V3=(3xcm)3=(33)(x3)=27x3cm3
V4=(4xcm)3=(43)(x3)=64x3cm3
V1+V2+2V3=x3+8x3+2(27x3)=x3+8x3+54x3=63x3
- Compare with V4:
63x3<64x3(True)
V1+4V2+V3=x3+4(8x3)+27x3=x3+32x3+27x3=60x3
- Compare with V4:
60x3<64x3(True)
2(V1+V3)+V2=2(x3+27x3)+8x3=2(28x3)+8x3=56x3+8x3=64x3
- Compare with V4:
64x3=64x3(True)
All statements (1, 2, and 3) are correct.
Topper's Solved these Questions
- IMO QUESTION PAPER 2017 SET ABOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2017 SET AEXERCISE - Everyday Mathematics
10 Videos
- IMO QUESTION PAPER 2016 SET BBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2016 SET BEXERCISE - ACHIEVERS SECTION
5 Videos
- IMO QUESTION PAPER 2017 SET-BBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2017 SET-BEXERCISE - Achievers Section
5 Videos
Similar Questions
V1, V2, V3 and V4 are the volumes of four cubes of side lengths x cm , 2x cm , 3x cm and 4x cm respectively. Some statements regarding these volumes are given below V1+V2+2V3<V4 (2) V1+4V2+V3<V4 (3) 2(V1+V3)+V2=V4 Which of these statements are correct? (a) 1 and 2 (b) 2 and 3 (c) 1 and 3 (d) 1, 2 and 3
View SolutionIf V1,V2 and V3 be the volumes of a right circular cone, a sphere and a right circular cylinder having the same radius and same height, then
View Solution
Knowledge Check
V1,V2,V3 are the volumes of four cubes of side lengths x cm, 2x cm, 3x cm and 4x cm respectively. Some statements regarding these 4 volumes are shown here.
(1) V1+V2+2V3<V4 (2) V1+4V2+V3<V4 (3) 2(V1+V3)+V2=V4
Which of the given statements are correct?A(1) and (2) onlyB(2) and (3) onlyC(1) and (3) onlyD(1), (2) and (3)If V1andV2 are the volume of one gm water at 0∘Cand4∘C respectively, then :
AV1>V2BV1=V2CV1>V2DV1≤V2A constant pressure V1 and V2 are the volumes of a given mass of a gas at temperature 27∘C and 54∘C respectively. Then the ratio V1V2 will be
A100109B(√100109)C1054D5410
Each edge of two cubes are 2 cm and 4 cm and their volumes are v1 and v2.find v1:v2.
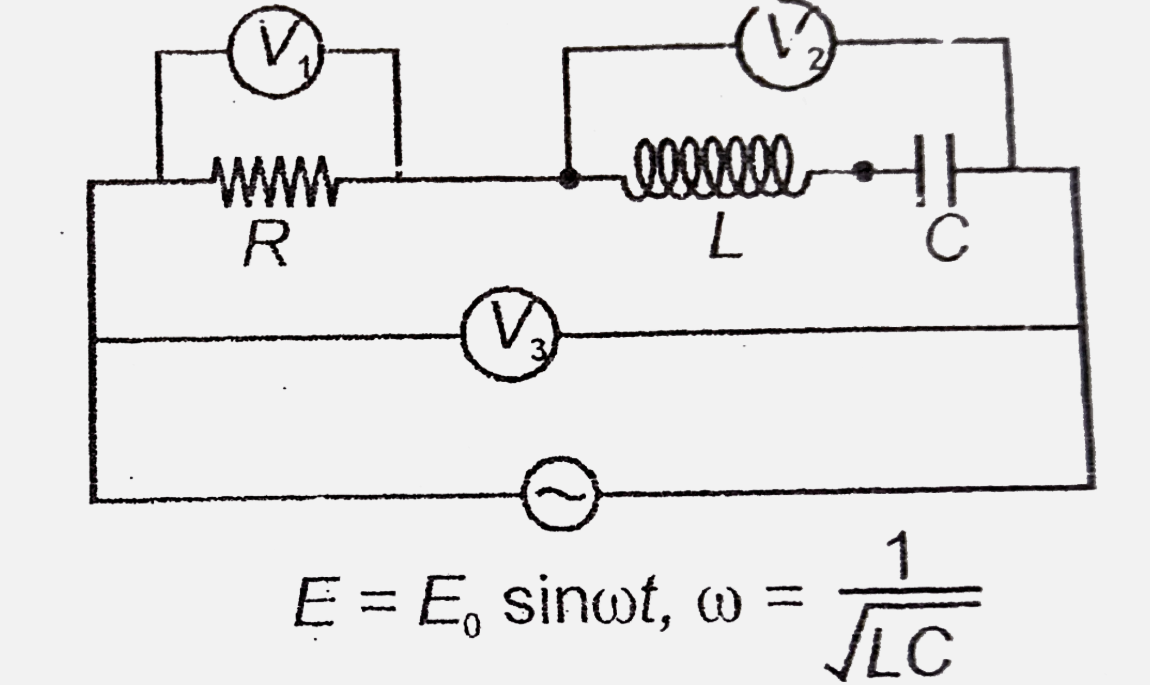
View SolutionIn the circuit shown, the readings of voltmeters V1,V2andV3 are given by
View SolutionIn the figure shown, i1=10e2tA , i2=4A and Vc=3e−2tV Determine
(a) iL and VL
(b) Vac , Vab and Vcd

View SolutionThe volume of a given mass of gas at 273K is x ? The volume of it at 200C is V20 .Then its volume at 250C is
(1) 25x
(2) V20+(25x)/(273)
(3) V20+(5x)/(273)
(4) V20X5x
View SolutionV1,V2 and V3 are the p.ds. across the 1Ω,2Ω and 3Ω resistors in the following diagram, and the current is 5A.
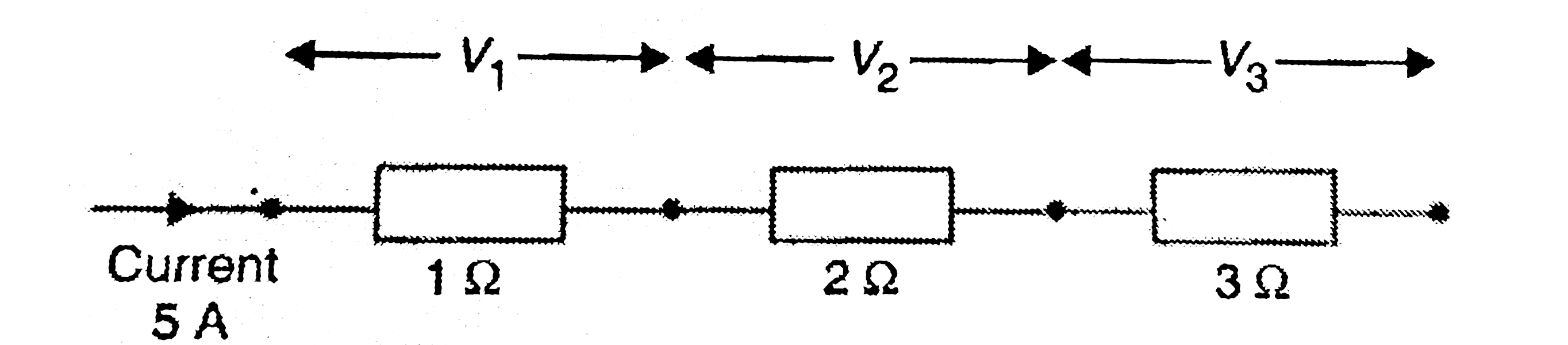
Which one of the columns (a) to (d) shows the correct values of V1,V2 and V3 measured in volts?
View Solution
