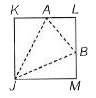
In the given figure. JKLM is a square with sides of length 6 units. Points A and B are the mid-points of sides KL and LM respectively. If a point is selected at random from the interior of the square. What is the probability that the point will be chosen from the interior of ΔJAB?
5/8
7/8
3/4
3/8
The correct Answer is:D
Step by step video, text & image solution for In the given figure. JKLM is a square with sides of length 6 units. Points A and B are the mid-points of sides KL and LM respectively. If a point is selected at random from the interior of the square. What is the probability that the point will be chosen from the interior of DeltaJAB? by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - PROBABILITYEXERCISE - EVERYDAY MATHEMATICS4videos
PROBABILITY
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - POLYNOMIALS EXERCISE - ACHIEVERS SECTION ( HOTS)3videos
POLYNOMIALS
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - QUADRATIC EQUATIONSEXERCISE - Achievers Section (HOTS)3videos
QUADRATIC EQUATIONS
Similar Questions
In the Fig. 13.12, JKLM is a square with sides of length 6 units. Points A and B are the mid-points of sides KL and LM respectively. If a point is selected at random from the interior of the square. What is the probability that the point will be chosen from the interior of JAB ? (FIGURE)
View SolutionA point is selected at random from the interior of a circle. The probability that the point is closer to the centre than the boundary of the circle is
View Solution
Knowledge Check
- Question 1 - Select One
A point is selected randomly from the interior of a circle. The probability that the point is closer to the centre, then the boundary of circle is
A34B14C12D23 - Question 2 - Select One
OPQR is a square with M and N as the middle points of the sides PQ and QR, respectively. The ratio of the areas of the square and the triangle OMN is
A4:1B2:1C8:3D4:3 - Question 3 - Select One
Let □PQRS be a quadrilateral. If M and N are the mid-points of the sides PQ and RS respectively, then PS+QR=
A3¯¯¯¯¯¯¯¯MNB4¯¯¯¯¯¯¯¯MNC2¯¯¯¯¯¯¯¯MND2¯¯¯¯¯¯¯¯NM
In the given figure, A, B, C and D are centres of four circles that have a radius of 1 unit. If a point is selected at random from interior of square ABCD, then what is the probability that it lies in the shaded region
View SolutionIn the figure given below, ABCD is a square of side 14 cm with E, F, G and H as the mid points of sides AB, BC, CD and DA respectively. The area of the shaded portion is
 View Solution
View SolutionIn the figure given below, ABCD is a square of side 14 cm with E,F,G and H as the mid points of sides. The area of EFGH is :
 View Solution
View SolutionTwo squares of 1×1 are chosen at random on a chestboard. What is the probability that they have a side in common ?
View SolutionOPQR is a square with M and N as the middle points of the sides PQ and QR, respectively. The ratio of the areas of the square and the triangle OMN is
View Solution
