Find the value of p and q respectively which satisfies the given equation.
p13+q13=723
4,8
2,3
3,4
3,5
The correct Answer is:C
To solve the equation p13+q13=723, we will follow these steps:
Step 1: Convert the mixed fraction on the right-hand side to an improper fraction.
The mixed fraction 723 can be converted to an improper fraction using the formula:
Improper Fraction=(a×c+b)/c
where a is the whole number, b is the numerator of the fraction, and c is the denominator.
For 723:
- a=7
- b=2
- c=3
Using the formula:
723=7×3+23=21+23=233
Step 2: Rewrite the equation with the improper fraction.
Now we can rewrite the original equation:
p13+q13=233
Step 3: Combine the left-hand side.
The left-hand side can be combined:
p+q3=233
Step 4: Eliminate the denominator by multiplying both sides by 3.
Multiply both sides by 3 to eliminate the fraction:
p+q=23
Step 5: Find suitable values for p and q.
Now we need to find pairs of integers (p,q) that satisfy the equation p+q=23. We can check the options provided (if any) or find suitable pairs manually.
Step 6: Check possible pairs.
Let's consider pairs:
- If p=3, then q=20 (3 + 20 = 23)
- If p=4, then q=19 (4 + 19 = 23)
- If p=10, then q=13 (10 + 13 = 23)
- If p=11, then q=12 (11 + 12 = 23)
- If p=12, then q=11 (12 + 11 = 23)
- If p=13, then q=10 (13 + 10 = 23)
- If p=19, then q=4 (19 + 4 = 23)
- If p=20, then q=3 (20 + 3 = 23)
Conclusion:
From the calculations, the pairs (3,20),(4,19),(10,13),(11,12),(12,11),(13,10),(19,4),(20,3) all satisfy the equation p+q=23.
The mixed fraction 723 can be converted to an improper fraction using the formula:
Improper Fraction=(a×c+b)/c
where a is the whole number, b is the numerator of the fraction, and c is the denominator.
- a=7
- b=2
- c=3
723=7×3+23=21+23=233
Now we can rewrite the original equation:
p13+q13=233
The left-hand side can be combined:
p+q3=233
Multiply both sides by 3 to eliminate the fraction:
p+q=23
Now we need to find pairs of integers (p,q) that satisfy the equation p+q=23. We can check the options provided (if any) or find suitable pairs manually.
Let's consider pairs:
- If p=3, then q=20 (3 + 20 = 23)
- If p=4, then q=19 (4 + 19 = 23)
- If p=10, then q=13 (10 + 13 = 23)
- If p=11, then q=12 (11 + 12 = 23)
- If p=12, then q=11 (12 + 11 = 23)
- If p=13, then q=10 (13 + 10 = 23)
- If p=19, then q=4 (19 + 4 = 23)
- If p=20, then q=3 (20 + 3 = 23)
From the calculations, the pairs (3,20),(4,19),(10,13),(11,12),(12,11),(13,10),(19,4),(20,3) all satisfy the equation p+q=23.
Topper's Solved these Questions
- IMO QUESTION PAPER 2018-19 SET BBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2018-19 SET BEXERCISE - Everyday Mathematics
15 Videos
- IMO QUESTION PAPER 2018-19 SET ABOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2018-19 SET AEXERCISE - Achievers section
5 Videos
- IMO QUESTION PAPER 2019-20 SET ABOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2019-20 SET AEXERCISE - LOGICAL REASONING
1 Videos
Similar Questions
Find the values of p and q respectively for which the equation 2x2+px=q has root - 3 and factor (x-5).
View SolutionFind the values of p and q for which the following system of equations has infinite number of solutions: 2x+3y=7, (p+q)x+(2p−q)y=21
View SolutionFind the values of P, Q and X in the following equation: 7N14+2He4→PXQ+1H1.
View SolutionFind the value of p and q for which the following system of linear equations has infinite number of solutions: 2x+3y=1,(p+q)x+(2p−q)y=21.
View SolutionFind the values of p and q for which the following system of linear equations has infinite number of solutions: 2x+3y=9, (p+q)x+(2p−q)y=3(p+q+1)
View SolutionIf p and q are the roots of x2−ax+b=0, find the value of 1p3+1q3.
View SolutionFind the value of p for which the quadratic equation (p+1)x2+−6(p+1)x+3(p+9)=0,p≠−1 has equal roots. Hence, find the roots of the equation.
View SolutionIf (p−1q2p3q−2)13÷(p6q−3p−2q3)13=paqb, then the value of a+b where p and q are different positive primes is-
यदि (p−1q2p3q−2)13÷(p6q−3p−2q3)13=paqb है, तो a+b का मान क्या है जिसमें p और q विभिन्न धनात्मक अभाज्य है?
View SolutionThe value of p and q for whichp,q are the roots of the equation x2+px+q=0 are
View SolutionFind the value of p+q3 for given structure
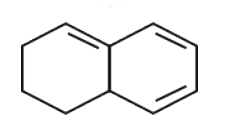
p = degree of unsturation (DU)
q = number of 2∘ carbon
View Solution
