Which of the following triangles is isosceles right angled triangle?
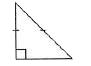
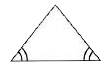
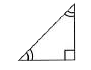
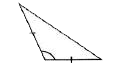
The correct Answer is:C
To determine which triangle is an isosceles right-angled triangle, we need to understand the properties of such triangles.
1. Understand the Definition:
- An isosceles triangle has at least two sides that are equal in length.
- A right-angled triangle has one angle that measures 90 degrees.
2. Identify the Characteristics:
- For a triangle to be an isosceles right-angled triangle, it must have:
- Two sides of equal length.
- One angle that is exactly 90 degrees.
3. Examine the Options:
- Look at the given triangles and check their angles and side lengths.
- You need to find a triangle that has:
- One angle measuring 90 degrees.
- The two sides that form this right angle must be equal in length.
4. Analyze Each Triangle:
- For each triangle option:
- Check if there is a right angle (90 degrees).
- Check if the two sides that form the right angle are of equal length.
5. Identify the Correct Triangle:
- After analyzing all the options, the triangle that meets both criteria (one right angle and two equal sides) is the isosceles right-angled triangle.
6. Conclusion:
- Based on the analysis, you can conclude which triangle is an isosceles right-angled triangle.
- An isosceles triangle has at least two sides that are equal in length.
- A right-angled triangle has one angle that measures 90 degrees.
- For a triangle to be an isosceles right-angled triangle, it must have:
- Two sides of equal length.
- One angle that is exactly 90 degrees.
- Look at the given triangles and check their angles and side lengths.
- You need to find a triangle that has:
- One angle measuring 90 degrees.
- The two sides that form this right angle must be equal in length.
- For each triangle option:
- Check if there is a right angle (90 degrees).
- Check if the two sides that form the right angle are of equal length.
- After analyzing all the options, the triangle that meets both criteria (one right angle and two equal sides) is the isosceles right-angled triangle.
- Based on the analysis, you can conclude which triangle is an isosceles right-angled triangle.
Topper's Solved these Questions
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - UNDERSTANDING ELEMENTARY SHAPESEXERCISE - ACHIEVERS SECTION (HOTS)5videos
UNDERSTANDING ELEMENTARY SHAPES
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - SYMMETRYEXERCISE - MATHEMATICAL REASONING15videos
SYMMETRY
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - WHOLE NUMBERSEXERCISE - Achievers section (HOTS)5videos
WHOLE NUMBERS
Similar Questions
Knowledge Check
- Question 1 - Select One
Which of the following are sides of an isosceles right triangle?
A3, 4, 5B3, 3, 4C12, 12, 5D4, 4, √32 - Question 2 - Select One or More
Which one of the following is correct in respect of a right-angled triangle ?
ASum of the two angles of a triangle is greater than the third angleBSum of the two angles of a triangle is less than the third angleCSum of the two angles of a triangle is equal to the third angleDNone of these - Question 3 - Select One
Which of the following holds for a right angle triangle ABC?
ADiameter of one of the ex-circles equals to the perimeter of the triangle.BDiameter of the circle circumscribing ΔABC equals to one of the sides of triangle.Cr:b+c:a=2:17:13DDiameter of incircle equals to length of the shortest tangent drawn from the vertices to the incircle
Which of the following can be the sides of a right angled triangle ?
View SolutionThe cosine of the obtuse angle formed by the medians from the vertices of the acute angles of an isosceles right angled triangle is
View SolutionIn the given figure, △ABC is an isosceles triangle right angled at C with AC = 4 cm. Find the length of AB.
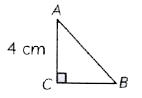View SolutionIn △ABC, if cosA+sinA−2cosB+sinB=0 then prove that triangle is isosceles right angled.
View SolutionIf triangle formed by medians of a right angled triangle is also a right angled triangle then what is the ratio of sides of the original right angled triangle ?
View Solution