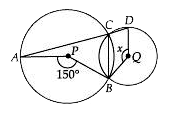
In the given figure, P and Qare centres of two circles, intersecting at B and C and ACD is a straight line. If ∠APB=150∘and∠BQD=x then find the value of x.
A
210∘
B
105∘
C
75∘
D
150∘
Video Solution
Text Solution
The correct Answer is:D
|
Answer
Step by step video, text & image solution for In the given figure, P and Qare centres of two circles, intersecting at B and C and ACD is a straight line. If angle APB = 150^(@) and angle BQD =x then find the value of x. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- IMO QUESTION PAPER 2017 SET BBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2017 SET BEXERCISE - EVERYDAY MATHEMATICS
10 Videos
- IMO QUESTION PAPER 2017 SET BBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2017 SET BEXERCISE - ACHIEVERS SECTION
5 Videos
- IMO QUESTION PAPER 2016 SET BBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2016 SET BEXERCISE - Achievers section
5 Videos
- IMO QUESTION PAPER 2018 SET ABOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2018 SET AEXERCISE - ACHIEVERS SECTION
5 Videos
Similar Questions
Knowledge Check
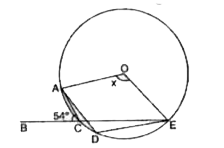
In the given figure, O is the centre of the circle, ∠ACB=54∘ and BCF is a straight line. Find x.
 A126∘B54∘C108∘D90∘
A126∘B54∘C108∘D90∘In the figure , A and C are the centres of the circles. DEB is a straight line. If relex angle BAF = 208∘ then obtuse angle DCF=
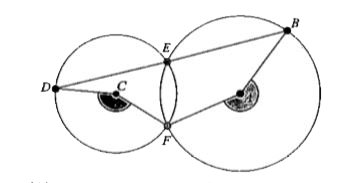 A152∘B176∘C120∘D150∘
A152∘B176∘C120∘D150∘Two circles with centres P and Q intersect at B and C, A, D are points on the circles with centres P and Q respectively such that A, C, D are colliner. If ∠APB=130∘,and∠BQD=x∘, then the value of x is :
A65B130C195D135
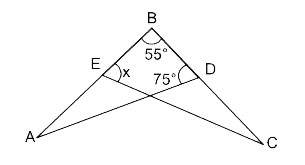
If APB is a straight line then find x
View SolutionIn the given figure , if AB=BC and ∠A=∠C then find the value of x
View SolutionIn the adjoining figure, ∠ABC=95∘ and ∠DAC=35∘, then find the value of ∠ACD.

View SolutionIn the given figure, O is the centre of the circle, ∠AOB=90∘. Find ∠APB :
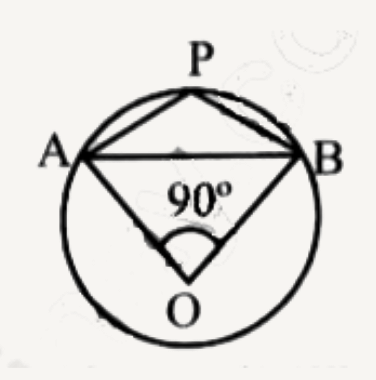
View SolutionIn the given figure, if O is the centre of the circle and PB = PC. If PQ is a straight line, then the value of x is
View Solution
