Without looking at any page, a number is chosen at random from the page. What is the probability that the digit at the units place of the number chosen is greater than 6 ?
310
610
410
None of these
The correct Answer is:A
To find the probability that the digit at the unit's place of a randomly chosen number is greater than 6, we can follow these steps:
Step 1: Identify the possible digits.
The digits at the unit's place can be any of the following:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Step 2: Count the total number of digits.
There are a total of 10 digits (0 through 9).
Step 3: Identify the digits greater than 6.
The digits that are greater than 6 are:
7, 8, 9.
Step 4: Count the number of favorable outcomes.
The number of favorable outcomes (digits greater than 6) is 3 (which are 7, 8, and 9).
Step 5: Calculate the probability.
The probability P that the digit at the unit's place is greater than 6 is given by the formula:
P=Number of favorable outcomesTotal number of outcomes=310
Final Answer:
The probability that the digit at the unit's place of the number chosen is greater than 6 is 310.
---
The digits at the unit's place can be any of the following:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
There are a total of 10 digits (0 through 9).
The digits that are greater than 6 are:
7, 8, 9.
The number of favorable outcomes (digits greater than 6) is 3 (which are 7, 8, and 9).
The probability P that the digit at the unit's place is greater than 6 is given by the formula:
The probability that the digit at the unit's place of the number chosen is greater than 6 is 310.
Topper's Solved these Questions
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - PROBABILITYEXERCISE - EVERYDAY MATHEMATICS4videos
PROBABILITY
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - PROBABILITYEXERCISE - ACHIEVERS SECTION (HOTS)3videos
PROBABILITY
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - POLYNOMIALSEXERCISE - ACHIEVERS SECTION (HOTS)3videos
POLYNOMIALS
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - QUADRILATERALSEXERCISE - Achievers Section (HOTS)3videos
QUADRILATERALS
Similar Questions
On one page of a telephone directory, there are 150 phone numbers. The frequency distribution of their unit digits is given below
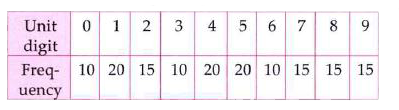
One of the numbers is chosen at random from the page. What is the probability that the unit digit of the chosen number is
greater than 8 ?View SolutionA digit is chosen at random from the digits 1 to 9. What is the probability that the digit is even?
View Solution
Knowledge Check
- Question 1 - Select One
On one page of a telephone directory , there were 200 phone numbers . The frequency distribution of their unit's digits is given below :
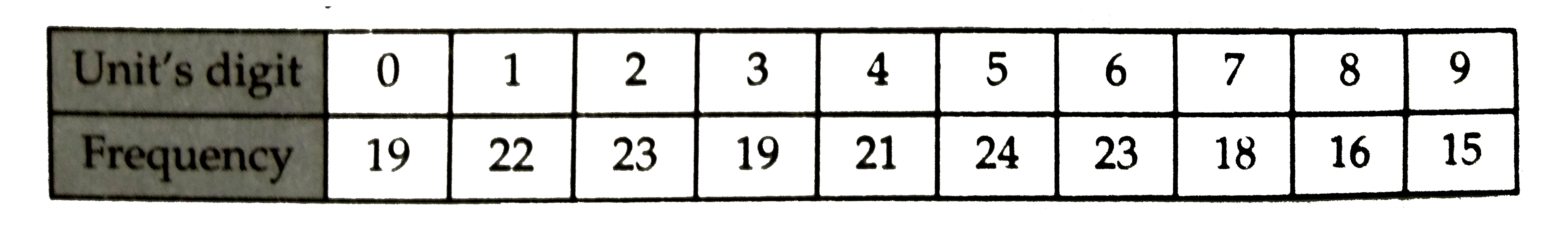
One of the numbers is chosen at random from the page . What is the probability that the unit's digit of the chosen number is (i) 5 ? (ii) 8 ?A(i) 0.02 (ii) 0.08B(i) 0.12 (ii) 0.18C(i) 0.1 (ii) 0.08D(i) 0.12 (ii) 0.08 - Question 2 - Select One
A natural number is chosen at random from the first 100 natural numbers. What is the probability that the number chosen is a multiple of 2 or 3 or 5?
A30100B133C74100D710 - Question 3 - Select One
Three numbers are chosen at random from 1 to 15. The probability that they are consecutive is
A1190B1120C135D575
One number is chosen at random from the numbers 1 to 21. What is the probability that it is prime?
View SolutionOn one page of a telephone directory, there are 150 phone numbers. The frequency distribution of their unit digits is given below
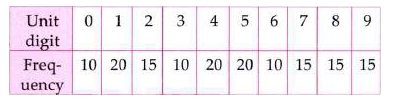
One of the numbers is chosen at random from the page. What is the probability that the unit digit of the chosen number is
less than 3 ?View SolutionA book contains 85 pages. A page is chosen at random. What is the probability that the sum of the digits on the page is 8?
View SolutionIf a number x is chosen at random from the numbers −2, −1, 0, 1, 2 . What is the probability that x2<2 ?
View SolutionIf a three digit number is chosen at random, what is the probability that the chosen number is amultiple of 2?
View Solution
