A hemispherical dome of a building needs to be painted from outside. If the circumference of the base of the dome is 17.6 m, then find the cost of painting it at the rate of Rs. 8 per 100 cm2
Rs. 35680
Rs. 28650
Rs. 39424
None of these
The correct Answer is:C
To solve the problem step by step, we need to find the surface area of the hemispherical dome and then calculate the cost of painting it based on the given rate.
Step 1: Find the radius of the hemispherical dome
The circumference C of the base of the dome is given as 17.6 m. The formula for the circumference of a circle is:
C=2πr
where r is the radius. We can rearrange this formula to find r:
r=C2π
Substituting the value of C:
r=17.62π
Using π≈3.14:
r=17.62×3.14≈17.66.28≈2.8 m
Step 2: Calculate the curved surface area of the hemispherical dome
The formula for the curved surface area A of a hemisphere is:
A=2πr2
Substituting the value of r:
A=2π(2.8)2
Calculating (2.8)2:
(2.8)2=7.84
Now substituting back:
A=2π×7.84≈2×3.14×7.84≈49.28 m2
Step 3: Convert the area from square meters to square centimeters
Since the cost of painting is given per 100 cm², we need to convert the area from m² to cm².
1 m² = 10,000 cm², so:
49.28 m2=49.28×10,000 cm2=492800 cm2
Step 4: Calculate the cost of painting
The cost of painting is given as Rs. 8 per 100 cm². First, we find the number of 100 cm² units in 492800 cm²:
Number of 100 cm2=492800100=4928
Now, calculating the total cost:
Total Cost=4928×8=39424 Rs.
Final Answer
The cost of painting the hemispherical dome is Rs. 39,424.
---
The circumference C of the base of the dome is given as 17.6 m. The formula for the circumference of a circle is:
C=2πr
where r is the radius. We can rearrange this formula to find r:
r=C2π
Substituting the value of C:
r=17.62π
Using π≈3.14:
r=17.62×3.14≈17.66.28≈2.8 m
The formula for the curved surface area A of a hemisphere is:
A=2πr2
Substituting the value of r:
A=2π(2.8)2
Calculating (2.8)2:
(2.8)2=7.84
Now substituting back:
A=2π×7.84≈2×3.14×7.84≈49.28 m2
Since the cost of painting is given per 100 cm², we need to convert the area from m² to cm².
1 m² = 10,000 cm², so:
49.28 m2=49.28×10,000 cm2=492800 cm2
The cost of painting is given as Rs. 8 per 100 cm². First, we find the number of 100 cm² units in 492800 cm²:
Number of 100 cm2=492800100=4928
Now, calculating the total cost:
Total Cost=4928×8=39424 Rs.
The cost of painting the hemispherical dome is Rs. 39,424.
Topper's Solved these Questions
- SURFACE AREAS AND VOLUMESBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - Achievers Section (HOTS)
3 Videos
- SURFACE AREAS AND VOLUMESBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - Achievers Section (HOTS)
3 Videos
- STATISTICSBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - STATISTICSEXERCISE - Achievers Section (HOTS)
3 Videos
- TRIANGLESBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - TRIANGLESEXERCISE - Achievers Section (HOTS)
2 Videos
Similar Questions
A hemispherical dome of a building needs to be painted (see Fig. 13.21). If the circumference of the base of the dome is 17.6 m, find the cost of painting it, given the cost of painting is Rs 5 per 100 cm2
View SolutionThe dome of a building is in the form of a hemisphere. Its radius is 63dm. Find the cost of painting it at the rate of Rs. 2 per sq.m.
View SolutionA wooden toy is in the form of a cone surmounted on a hemisphere. The diameter of the base of the cone is 5cm and its height is 4cm. Find the cost of painting the toy at the rate of Rs. 5 per 1000cm2.
View Solution10 cylindrical pillars of a building have to be painted. The diameter of each pillar is 70cm and the height is 4m. What is the cost of painting at the rate of Rs 5 per square metre
View Solution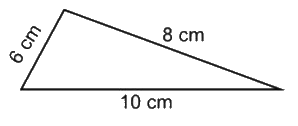
The cost of painting the given sign board at the rate of 9 paise per cm2 is
View SolutionThe sides of a triangle shaped sheet are 5cm, 12cm and 13cm. Find the cost of painting on the sheet at the rate of Rs 30 per cm2?
View SolutionThe edges of a triangular board are 6cm,8cm and 10cm .The cost of painting it at the rate of 9paiseper"cm2 is "
View SolutionA storage tank consists of a circular cylinder with a hemisphere adjoined on either end. If the external diameter of the cylinder be 1.4m and its length be 8m, find the cost of painting it on the outside at the rate of Rs. 10 per m2.
View SolutionThe side of a triangle shaped sheet are 5cm, 12cm and 13cm. Find the cost of painting on the sheet at the rate of Rs 30 per cm sq.
View SolutionA hemispherical bowl made of brass has inner diameter 10.5cm. Find the cost of tinplating it on the inside at the rate of Rs. 4 per 100 cm2
View Solution
