If lines AB, AC, AD and AE are parallel to a line l, then ________ .
A, B, C, D and E are collinear points.
A, B, C, D and E are non-collinear points.
Lines AB and AC are parallel and lines AD and AE are perpendicular.
None of these
The correct Answer is:A
To solve the problem, we need to analyze the given information about the lines and their relationships with line l.
1. Understanding Parallel Lines: We are given that lines AB, AC, AD, and AE are all parallel to a line l.
2. Definition of Parallel Lines: By definition, if two lines are parallel, they will never meet, no matter how far they are extended.
3. Transitive Property of Parallel Lines: If a line is parallel to another line, and a third line is also parallel to the first line, then the third line is also parallel to the second line. This means that if AB is parallel to l, and AC is also parallel to l, then AB is parallel to AC.
4. Applying the Property: Since all the lines (AB, AC, AD, and AE) are parallel to line l, we can conclude that:
- AB is parallel to AC
- AB is parallel to AD
- AB is parallel to AE
- AC is parallel to AD
- AC is parallel to AE
- AD is parallel to AE
5. Conclusion: Therefore, all lines AB, AC, AD, and AE are parallel to each other.
6. Co-linear Points: Since all these lines are parallel, the points A, B, C, D, and E must lie on the same line (which is the line that is parallel to l). Thus, we can conclude that A, B, C, D, and E are co-linear points.
Final Answer:
If lines AB, AC, AD, and AE are parallel to a line l, then A, B, C, D, and E are co-linear points.
- AB is parallel to AC
- AB is parallel to AD
- AB is parallel to AE
- AC is parallel to AD
- AC is parallel to AE
- AD is parallel to AE
If lines AB, AC, AD, and AE are parallel to a line l, then A, B, C, D, and E are co-linear points.
Topper's Solved these Questions
- IMO MODEL TEST PAPER - 1BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO MODEL TEST PAPER - 1EXERCISE - Everyday Mathematics
10 Videos
- IMO MODEL TEST PAPER - 1BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO MODEL TEST PAPER - 1EXERCISE - Achievers Section
5 Videos
- IMO MODEL TEST PAPER 2 BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO MODEL TEST PAPER 2 EXERCISE - Achievers Section
5 Videos
Similar Questions
Knowledge Check
Inside a triangle ABC, a straight line parallel to BC intersects AB and AC at the point P and respectively. If AB=3PB, then PQ:BC is
Aa) 1:3Bb) 3:4Cc) 1:2Dd) 2:3
Can you find whether the lines EF , GH , KP , AB and CD are parallel or not by using other conditions of parallel lines ?

View SolutionTwo chords AB and CD of a circle are parallel and a line l is the perpendicular bisector of AB. Show that l bisects CD
View SolutionTwo chords AB and CD of a circle are parallel and a line l is the perpendicular bisector of AB . Show that l bisects CD.
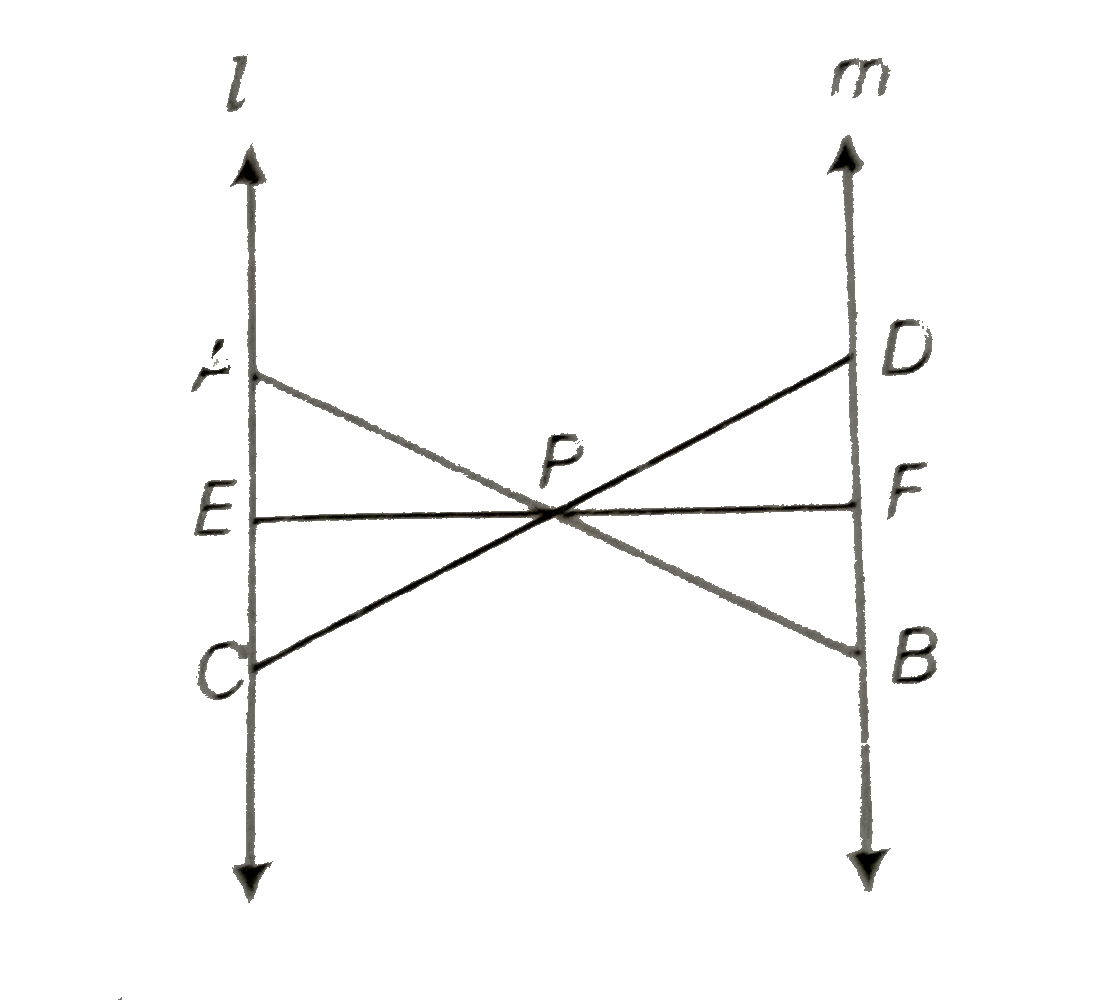
View SolutionIn given figure,l||m and liner segments AB, CD and EF are concurrent at point P. Prove that AEBF=ACBD=CEFD
View SolutionThe sides AB and AC are equal of an isosceles triangle ABC. D E and F are the mid-points of sides BC, CA and AB respectively. Prove that:
(i) Line segment AD is perpedicular to line segment EF.
(ii) Line segment AD bisects the line segment EF.
View SolutionIf a line intersects sides AB and AC of a ΔABCat D and E respectively and is parallel to BC, prove that ADAB=AEAC
View SolutionIn a ΔABC, if DE is drawn parallel to BC, cutting AB and AC to D and E respectively such that AB=7.2cm,AC=6.4cmandAD=4.5cm. Then, AE=?

View Solution