Study the given passage carefully &answer the questions in a sport Academy XY', there are some student who can play three games i.e tennis, cricket & chess. Total number of players who play tennis is 160 & all three games are played by 10% of total tennis players. Ratio of cricket to chess players is 3:5 and total of cricket & chess players is 100% more than tennis players. Players who play both tennis and chess are 1212% of total tennis players. Ratio of players who play both tennis & cricket to players who play both chess & cricket is 2:3 & total of players who play both tennis & cricket and players who play both chess & cricket is equal to one-fourth of chess players.
What is the difference between no. of players who can play tennis & players who play only cricket?
74
64
68
None of these
The correct Answer is:A
To solve the problem step by step, we will analyze the information provided and use a Venn diagram to organize the data.
Step 1: Determine the number of players playing all three games
The total number of players who play tennis is given as 160. According to the problem, 10% of these players play all three games (tennis, cricket, and chess).
Calculation:
- Players who play all three games = 10% of 160
- = 0.10 × 160 = 16
Step 2: Set up the Venn diagram
We will create a Venn diagram with three circles representing tennis, cricket, and chess. We will place the number of players who play all three games (16) in the intersection of all three circles.
Step 3: Analyze the ratio of cricket to chess players
The ratio of cricket to chess players is given as 3:5. Let’s denote the number of cricket players as 3x and the number of chess players as 5x.
Step 4: Total of cricket and chess players
It is stated that the total number of cricket and chess players is 100% more than the number of tennis players. Since the number of tennis players is 160, 100% more means:
Calculation:
- Total cricket and chess players = 160 + 160 = 320
From the ratio we set up:
- 3x + 5x = 320
- 8x = 320
- x = 40
Thus, the number of cricket players (3x) is:
- Cricket players = 3 × 40 = 120
And the number of chess players (5x) is:
- Chess players = 5 × 40 = 200
Step 5: Players who play both tennis and chess
It is given that players who play both tennis and chess are 12.5% of total tennis players.
Calculation:
- Players who play both tennis and chess = 12.5% of 160
- = 0.125 × 160 = 20
Step 6: Players who play both tennis and cricket and chess and cricket
The ratio of players who play both tennis & cricket to players who play both chess & cricket is given as 2:3. Let’s denote:
- Players who play both tennis & cricket = 2y
- Players who play both chess & cricket = 3y
Step 7: Total of players who play both tennis & cricket and chess & cricket
It is also stated that the total of players who play both tennis & cricket and players who play both chess & cricket is equal to one-fourth of chess players.
Calculation:
- Total of both = 2y + 3y = 5y
- One-fourth of chess players = 1/4 × 200 = 50
Thus, we have:
- 5y = 50
- y = 10
So, the number of players who play both tennis & cricket is:
- Players who play both tennis & cricket = 2y = 2 × 10 = 20
And the number of players who play both chess & cricket is:
- Players who play both chess & cricket = 3y = 3 × 10 = 30
Step 8: Calculate the number of players who play only cricket
To find the number of players who play only cricket, we need to subtract those who play both cricket and tennis and those who play both cricket and chess from the total number of cricket players.
Calculation:
- Total cricket players = 120
- Players who play both cricket & tennis = 20
- Players who play both chess & cricket = 30
So, players who play only cricket = Total cricket players - (Players who play both cricket & tennis + Players who play both chess & cricket + Players who play all three games)
- = 120 - (20 + 30 + 16)
- = 120 - 66
- = 54
Step 9: Calculate the difference between players who can play tennis and players who play only cricket
The total number of players who can play tennis is 160. We have already calculated that the number of players who play only cricket is 54.
Calculation:
- Difference = Players who play tennis - Players who play only cricket
- = 160 - 54
- = 106
Final Answer
The difference between the number of players who can play tennis and the players who play only cricket is 106.
---
The total number of players who play tennis is given as 160. According to the problem, 10% of these players play all three games (tennis, cricket, and chess).
- Players who play all three games = 10% of 160
- = 0.10 × 160 = 16
We will create a Venn diagram with three circles representing tennis, cricket, and chess. We will place the number of players who play all three games (16) in the intersection of all three circles.
The ratio of cricket to chess players is given as 3:5. Let’s denote the number of cricket players as 3x and the number of chess players as 5x.
It is stated that the total number of cricket and chess players is 100% more than the number of tennis players. Since the number of tennis players is 160, 100% more means:
- Total cricket and chess players = 160 + 160 = 320
- 3x + 5x = 320
- 8x = 320
- x = 40
- Cricket players = 3 × 40 = 120
- Chess players = 5 × 40 = 200
It is given that players who play both tennis and chess are 12.5% of total tennis players.
- Players who play both tennis and chess = 12.5% of 160
- = 0.125 × 160 = 20
The ratio of players who play both tennis & cricket to players who play both chess & cricket is given as 2:3. Let’s denote:
- Players who play both tennis & cricket = 2y
- Players who play both chess & cricket = 3y
It is also stated that the total of players who play both tennis & cricket and players who play both chess & cricket is equal to one-fourth of chess players.
- Total of both = 2y + 3y = 5y
- One-fourth of chess players = 1/4 × 200 = 50
- 5y = 50
- y = 10
- Players who play both tennis & cricket = 2y = 2 × 10 = 20
- Players who play both chess & cricket = 3y = 3 × 10 = 30
To find the number of players who play only cricket, we need to subtract those who play both cricket and tennis and those who play both cricket and chess from the total number of cricket players.
- Total cricket players = 120
- Players who play both cricket & tennis = 20
- Players who play both chess & cricket = 30
- = 120 - (20 + 30 + 16)
- = 120 - 66
- = 54
The total number of players who can play tennis is 160. We have already calculated that the number of players who play only cricket is 54.
- Difference = Players who play tennis - Players who play only cricket
- = 160 - 54
- = 106
The difference between the number of players who can play tennis and the players who play only cricket is 106.
Topper's Solved these Questions
- DATA INTERPRETATIONBOOK - ADDA247CHAPTER - DATA INTERPRETATIONEXERCISE - Mains Questions
33 Videos
- DATA INTERPRETATIONBOOK - ADDA247CHAPTER - DATA INTERPRETATIONEXERCISE - Previous Year Questions
56 Videos
- DATA INTERPRETATIONBOOK - ADDA247CHAPTER - DATA INTERPRETATIONEXERCISE - Prelims Questions (Level-1)
54 Videos
- BOAT AND STREAM BOOK - ADDA247CHAPTER - BOAT AND STREAM EXERCISE - Previous Year Question
22 Videos
- DATA SUFFICIENCY BOOK - ADDA247CHAPTER - DATA SUFFICIENCY EXERCISE - PREVIOUS YEAR QUESTIONS
25 Videos
Similar Questions
The pie chart given below shows the number of students who play five sports like Hockey, Tennis Cricket, Golf and Polo. The total number of students is 1080.
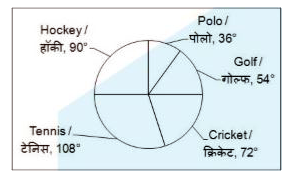
What is the difference between the number of students who play Tennis and those who play Polo?
View Solution66 games were played in a tournament where each player placed one against the rest. The number of players are
View Solution
Knowledge Check
Comprehension:
Study the following diagram and answer questions based on it.
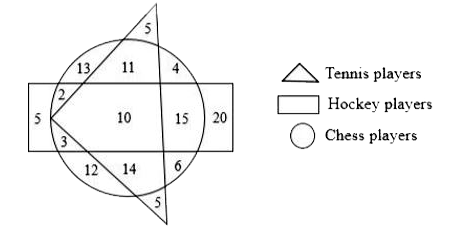
The number of non-chess players is how much more than the players who play both chess and tennis.A5B10CIt is the sameDCannot be determinedIn a group of 60 persons, 40 persons like play cricket and 10 persons like play both Tennis and Cricket. Then, the number of persons who like to play Tennis, is
A20B25C30D40In a group of 60 persons, 40 persons like play cricket and 10 persons like play both Tennis and Cricket. Then, the number of persons who like to play Tennis, is
A20B25C30D40
Study the following diagram and answer questions based on it.
The number of Non-Chess players is how much more than the players who play both Chess and Tennis?
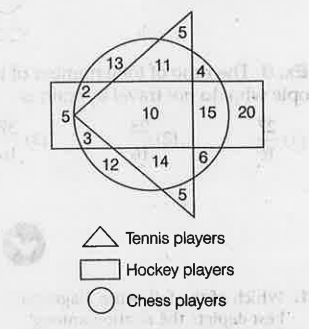
View Solution30 Cricketers and 20 Kho-kho players are training on a field. What is the ratio of cricketers to the total number of players ?
View SolutionIn a group of 100 people, 60 people like to play cricket, 20 people like to play both cricket and Tennis. How many people like to play Tennis but not cricket?
View SolutionThe pie chart given below shows the number of students who play five sports like Hockey, Tennis Cricket, Golf and Polo. The total number of students is 1080.

What is the average number of students playing Tennis and Cricket?
View Solution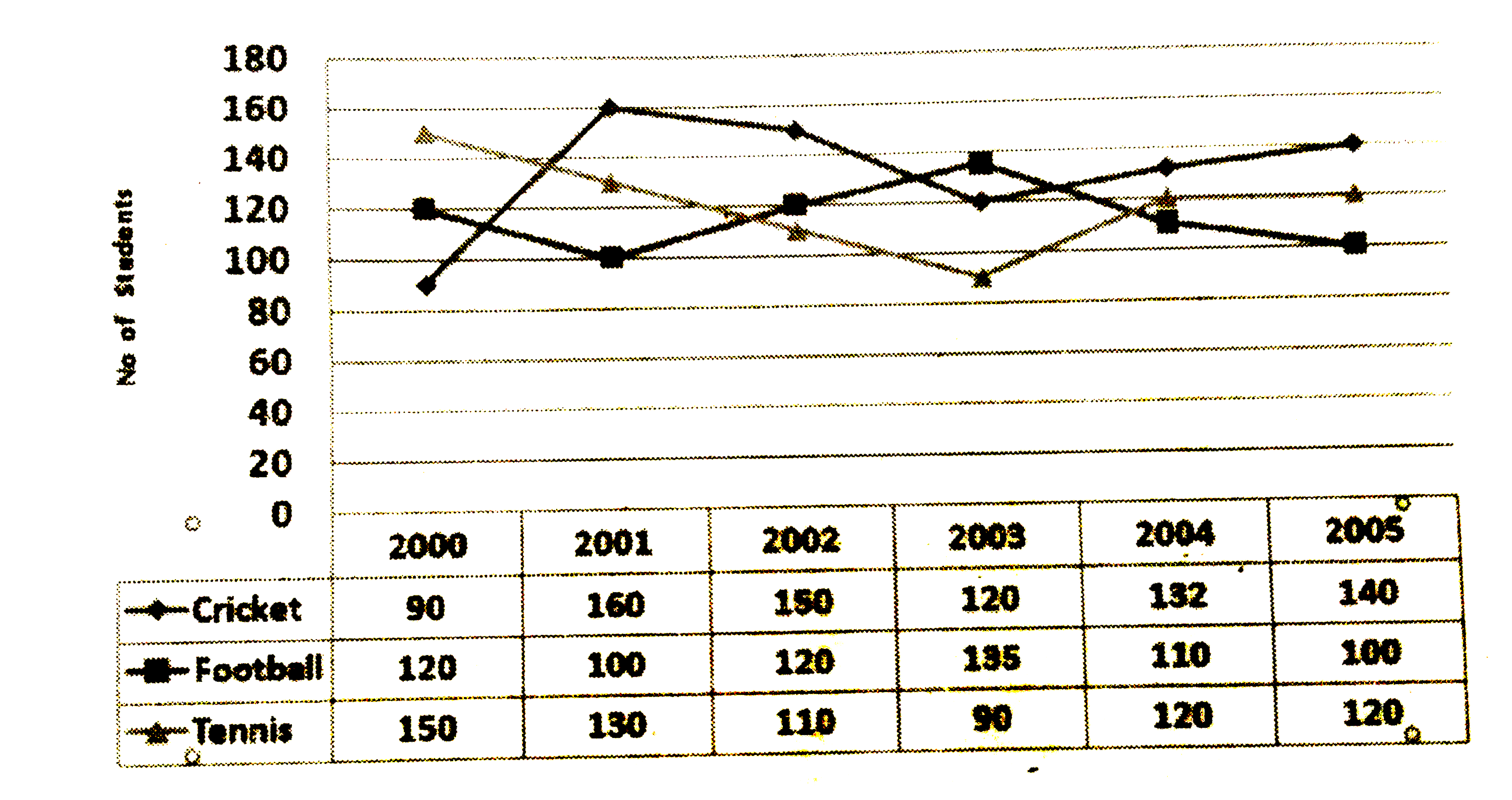
The total no of players who participated in all the 3 sports together in the year 2004 was What % of the total no of players who participates in Tennis over all years together (approx) ?
View Solution
