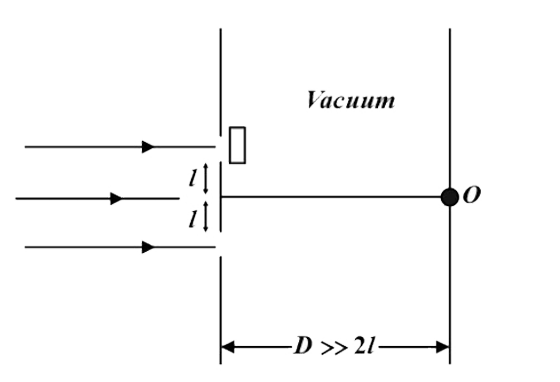
In young's double-slit experiment, both the slits produce equal intensities on a screen. A 100% transparent thin film of refractive index μ=1.5 is kept in front of one of the slits, due to which the intensity at the point O on the screen becomes 75% of its initial value. If the wavelength of monochromatic light is 720 nm, then what is the minimum thickness (in nm) of the film?
The correct Answer is:240
The path difference at the point O is:
Δx=(μ−1)t
I=4I0cos2(ϕ2)
0.75(4I0)=4I0cos2(ϕ2)
⇒ϕmin=60∘
ϕmin=2πλΔx=2πλ(μ−1)t=π3
t=λ6(μ−1)=λ06(1.5−1)=240nm
Topper's Solved these Questions
Similar Questions
Youngs Double slit experiment | variation of intensity on screen
View SolutionIn Young's double slit experiment the two slits are illuminated with light of wavelength λ .The thickness of a film of refractive index 1.4 to be introduced in the path of one of the interfering beams so that the central image shifts by one fringe width is
View Solution
Knowledge Check
In a Young's double slit experiment, the central point on the screen is
ABrightBDarkCFirst bright and then darkDFirst dark and then brightIn YDSE, both slits produce equal intensities on the screen. A 100% transparent thin film is placed in front of one of the slits. Now, the intensity on the centre becomes 75% of the previous intensity. The wavelength of light is 6000Å and refractive index of glass is 1.5. Thus, minimum thickness of the glass slab is
A0.2μmB0.3μmC0.4μmD0.5μmIn Young's double-slit experment, the frist maxima is observed at a fixed point P on the screen. Now, the screen is continously moved away from the plane of slits. The ratio of intensity at point P to the intensity at point O (center of the screen)
 Aremains cosntantBkeeps on decreasingCfirst decreases and then increasesDfirst decreases and then becomes constant
Aremains cosntantBkeeps on decreasingCfirst decreases and then increasesDfirst decreases and then becomes constant
A thin glass plate of thickness t and refractive index μ is inserted between screen and one of the slits in a young's experiment. If the intensity at the centre of the screen is I, what was the intensity at the same point prior to the introduction of the sheet.
View SolutionIn Young's double-slit experiment, let A and B be the two slit. A thin film of thickness t and refractive index μ is placed in front of A. Let β= fringe width. Then the central maxima will shift
View SolutionIn a young's double slit experiment ,let Aand B be the two slits.A thin film film of thickness t and refractive indexμ is pklaced in front of A.Let β =fringe width.The central maximum will shift:
View SolutionIn Young's double slit experiment, the distance between the two slits is 0.1 mm, the distance between the slits and the screen is 1 m and the wavelength of the light used is 600 nm. The intensity at a point on the screen is 75% of the maximum intensity. What is the smallest distance of this point from the central fringe ?
View SolutionIn Young's double slit experiment with light of wavelength λ=600nm, intensity of central fringe is I0. Now one of the slit is covered by glass plate of refractive index 1.4 and thickness t=5μm. The new intensity at the same point on screen will be :
View Solution
