The values of the mode and median are 7.52 and 9.06. respectively, in a moderately asymmetrical distribution. The mean of the distribution is:
9.83
8.67
10.23
9.5
The correct Answer is:A
To find the mean of a moderately asymmetrical distribution when the mode and median are given, we can use the empirical relationship between these three measures of central tendency.
1. Identify the given values:
- Mode (Mo) = 7.52
- Median (Me) = 9.06
2. Use the empirical relationship:
In a moderately asymmetrical distribution, the relationship between the mean (M), median (Me), and mode (Mo) can be approximated by the formula:
M=Mo+2×Me3
3. Substitute the values into the formula:
M=7.52+2×9.063
4. Calculate the value inside the parentheses:
- First, calculate 2×9.06:
2×9.06=18.12
- Now, add the mode:
7.52+18.12=25.64
5. Divide by 3 to find the mean:
M=25.643≈8.5467
6. Final result:
The mean of the distribution is approximately 8.55 (rounded to two decimal places).
- Mode (Mo) = 7.52
- Median (Me) = 9.06
In a moderately asymmetrical distribution, the relationship between the mean (M), median (Me), and mode (Mo) can be approximated by the formula:
M=Mo+2×Me3
M=7.52+2×9.063
- First, calculate 2×9.06:
2×9.06=18.12
- Now, add the mode:
7.52+18.12=25.64
M=25.643≈8.5467
The mean of the distribution is approximately 8.55 (rounded to two decimal places).
Similar Questions
Knowledge Check
For a moderately skewed distribution
AM.D.=Q.D.BS.D.=M.D.CQ.D.=2/3 σDM.D.=4/5 σIn a moderately asymmetrical distribution, the mean is 18 and median 22, the value of mode is
A30B10C4Dnone of theseIf the mean and median are 25 and 28 respectively, then find the value of the mode.
A35B34C36D134
Consider the following frequency distribution
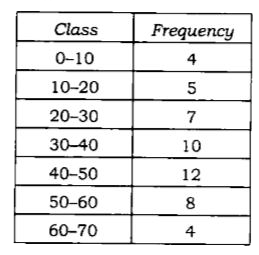
What is the median of the distribution?
View SolutionIf the mean and median are 25 and 28 respectively, then find the value of the mode.
View SolutionIf the mean and median of a set of numbers are 8.9 and 9 respectively then the mode will be
View SolutionIn a moderately skewed distribution, the values of mean and median are 5 and 6, respectively. The value of mode in such a situation is approximately equal to
View SolutionIin a moderately skewed distribution the values of mean and median are 5 and 6 respectively. The value of mode in such a situation is approximately equal to
View Solution