ΔOAB में, −−→OA=ˆi−ˆj+ˆk,−−→OB=ˆi+ˆj−ˆk ΔOAB का क्षेत्रफल ज्ञात करें।
The correct Answer is:√2 वर्ग इकाई
Step by step video, text & image solution for DeltaOAB में, vec(OA) = hati-hatj+hatk, vec(OB) = hati+hatj-hatk DeltaOAB का क्षेत्रफल ज्ञात करें। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
यदि A=[231−4] तथा B=[1−2−13] तो दिखलाएँ कि (AB)−1=B−1A−1
View SolutionIf →r=3ˆi+2ˆj−5ˆk,→a=2ˆi−ˆj+ˆk,→b=ˆi+3ˆj−2ˆk and→c=2ˆi+ˆj−3ˆk such that ˆr=x→a+y→b+z→c then
View Solutionयदि →a=ˆi+ˆj−ˆk,→b=ˆi−2ˆj+ˆk,→c=ˆi−ˆj−ˆk तब →a व →b के तल में वह सदिश जिसके →c पर परपेक्ष का मापक (1√3) है होगा-
View Solutionदिखाए गए वेक्टर −−→OA को ˆi,ˆj,ˆk पदों में लिखे.
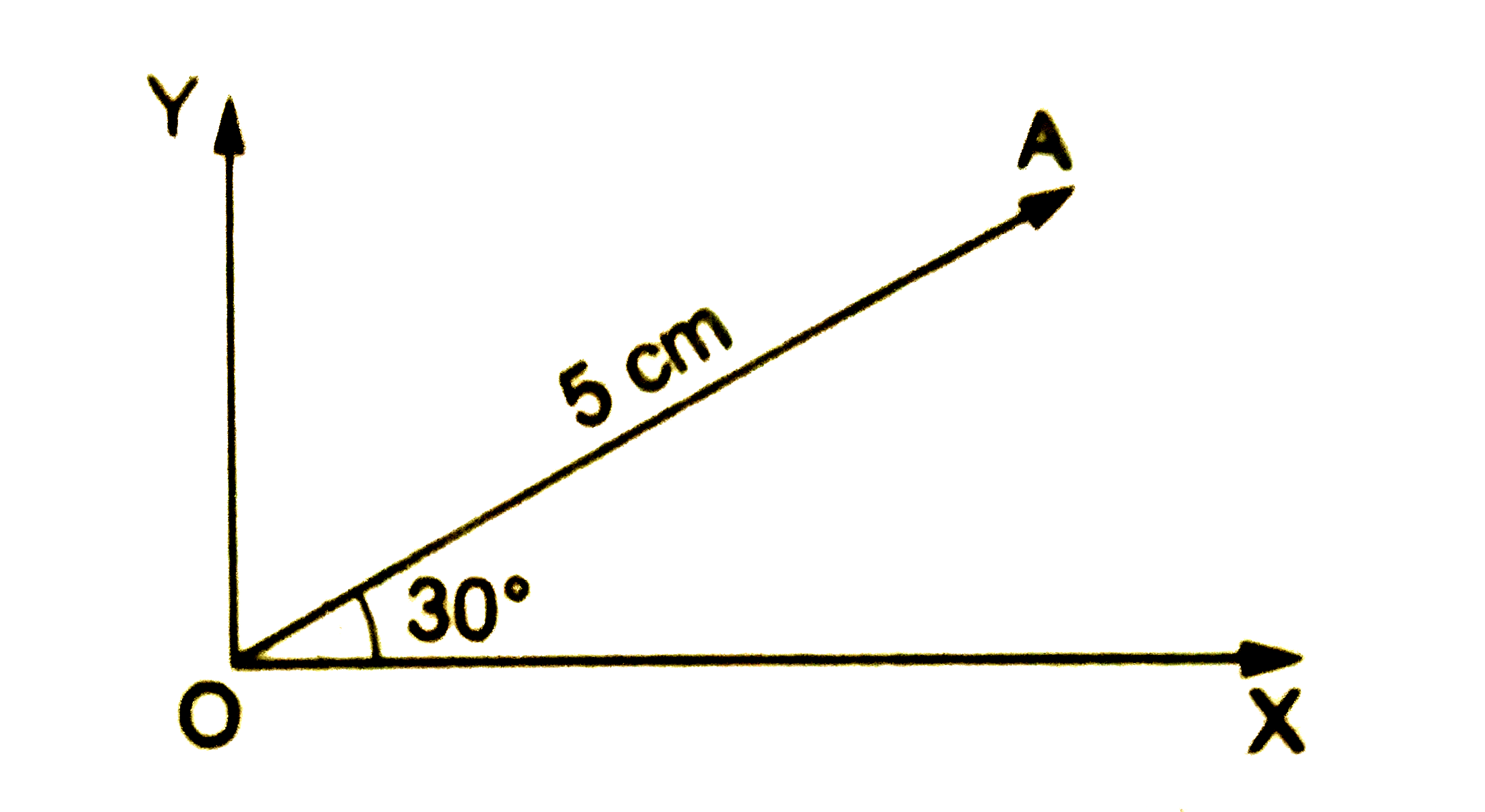
View SolutionGiven : vec A = hati + hatj +hatk and vec B =-hati-hatj-hatk What is the angle between (vec A - vec B) and vec A ?
View SolutionIf vector →a=ˆi+ˆj+ˆk,→b=4ˆi+3ˆj+4ˆk and →c=ˆi+αˆj+βˆk are linearly dependent and |→c|=√3 , then value of |α|+|β| is
View SolutionIf →a=ˆi−ˆj+ˆk,→b=2ˆi+ˆj−ˆkand→c=λˆi−ˆj+λˆk are coplanar, find the value of λ.
View SolutionFind the shortest distance and the vector equation of the line of shortest distance between the lines given by :
(i)→r=(−4ˆi+4ˆj+ˆk)+λ(ˆi+ˆj−ˆk)
and →r=(−3ˆi−8ˆj−3ˆk)+μ(2ˆi+3ˆj+3ˆk)
(ii)→r=(−ˆi+5ˆj)+λ(−ˆi+ˆj+ˆk)
and →r=(−ˆi−3ˆj+2ˆk)+μ(3ˆi+2ˆj+ˆk).
View SolutionFind the angle between the following pairs of lines :
(i)→r=2ˆi−5ˆj+ˆk+λ(3ˆi+2ˆj+6ˆk) and
→r=7ˆi−6ˆk+μ(ˆi+2ˆj+2ˆk)
(ii) →r=3ˆi+ˆj−2ˆk+λ(ˆi−ˆj−2ˆk) and
→r=2ˆi−ˆj−56ˆk+μ(3ˆi−5ˆj−4ˆk).
View SolutionFind the shortest distance betwee the lines :
→r=(ˆi+2ˆj+ˆk)+λ(ˆi−ˆj+ˆk) and
→r=2ˆi−ˆj−hakt+μ(2ˆi+ˆj+2ˆk).
View SolutionIf →α=2ˆi+3ˆj−ˆk,→β=−ˆi+2ˆj−4ˆk,→λ=ˆi+ˆj+ˆk, then (→α×→β).(→α×→γ) is :
View Solutionमाना →a=ˆi+ˆj+ˆk,→b=ˆi−ˆj+2ˆk और →c=xˆi+(x−2)ˆj−ˆk. यदि सदिश →c,→a और →b के समतल में स्थित है, तब x बराबर है
View Solutionसदिश →a,→b तथा →a×(→b×→a)………… है।
View SolutionFind angle θ between the vectors →a=ˆi+ˆj−ˆkand→b=ˆi−ˆj+ˆk.
View SolutionIn a parallelogram ABCD, −−→AB=ˆi+ˆj+ˆk and diagonal −−→AC=ˆi−ˆj+ˆk then ∠BAC = …………….
View SolutionIf →u=ˆi×(→a׈i)+ˆj×(→a׈j)+ˆk×(→a׈k) then →u = ………..
View Solution
