Question

हाइजेंस के द्वितीय तरंगिका सिद्धांत को लिखें।

Explanation

हाइगेंस का सिद्धान्त-(a) तरंगाग्र पर स्थित प्रत्येक बिन्दु एक नये तरंग स्रोत की तरह कार्य करता है जिससे निकलने वाली द्वितीयक तरंगिकायें सभी दिशाओं में फैल जाती है तथा मूल तरंग की चाल से गमन करती हैं।
(b) किसी भी क्षण सभी द्वितीयक तरंगिकाओं को स्पर्श करते हुए खींचा गया पृष्ठ उस क्षण पर तरंगान की नवीन स्थिति को प्रदर्शित करता है।
प्रकाश के किसी बिन्दु-स्रोत के समान दूरी पर चारों तरफ ईथर के कणों के कंपन की कलाएँ समांगी माध्यमों में समान होती है। वैसे समान-कंपन वाला कणों को स्पर्श करती हुई काल्पनिक सतह को तरंगाग्र कहा जाता है। समांगी माध्यमों में बिन्दु-स्रोतों के लिए तरंगाग्र गोलाकार होते हैं। बिन्दु स्रोतों से तरंग के संचरण को उस स्रोत से उत्पन्न गोलाकार तरंगान के प्रसार के रूप में व्यक्त किया जाता है।
चित्रानुसार-समय के बढ़ने के साथ सोत से निकला तरंगाग्र आगे की तरफ प्रसारित होता जाता है और इसके पहले वाले स्थानों पर दूसरे तरंगाग्र प्रसारित होकर आते-आते हैं। बिन्दु-स्रोत से निकली किरणें गोलाकार तरंगानों की त्रिज्याएँ होती हैं। अतः प्रकाश की किरणें इसके तरंगायों पर अभिलम्ब होती हैं। गोलीय तरंगाग्र संकेन्द्री वृत्तों द्वारा प्रदर्शित हैं।

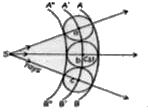
माना कि एक गोलीय सतह `sigma` है, जिसका केन्द्र बिन्दु स्रोत है जो प्रकाश का पल्स उत्सर्जित करता है। `t=0` समय में `sigma` पर प्रकाशीय विक्षोभ का कण पहुँचता है तथा कम समयावधि के लिए अन्त करता है जिसमें धनात्मक तथा ऋणात्मक विक्षोभ उत्पन्न होता है। `sigma` पर के ये कणें तब गोलीय तरंगिकाएँ भेजते हैं जो के चारों तरफ फैल जाते हैं। t समय में इन तरंगिकाओं में प्रत्येक को त्रिज्याएँ होती हैं। गोलीय `Sigma` सभी द्वितीयक तरंगिकाओं के ज्यामितीय आरेख हैं जो प्राथमिक तरंगाग्र `sigma` से t = 0 समय में उत्सर्जित हुए थे।
यह स्पष्ट है कि `Sigma` के बगल के बिन्दु पर बहुत से द्वितीयक तरंगिकाएँ केवल धनात्मक विक्षोभ पर मिलती हैं। इसलिए `sigma` से द्वितीयक तरंगिकाएँ इस प्रकार अध्यारोपित होती हैं कि वे द्वितीयक तरंगिकाओं के ज्यामितीय आरेख पर नये तरंगाग उत्पन्न करते हैं। इस प्रकार "सतह के बहुत से बिन्दुओं, जो कि तरंगाग्र द्वारा पहुँचते हैं, द्वितीयक तरंगिकाओं के स्रोत हो जाते हैं। किसी दिये गये बाद के समय में इन तरंगिकाओं के ज्यामितीय आरेख उस समय के तरंगान के नया स्थान द्वारा प्रदर्शित होता है।"