If a, b, c, d and e are positve numbers, and it is given that ,
a+b=c+db+d=2ad+e>a+bandc+d>a+e
then, which of the following statement is true ?
A
d>a>b>e>c
B
d>b>e>a>c
C
a>b>c>d>e
D
a>bb>e>c
Video Solution
Text Solution
The correct Answer is:A
a+b=c+b (i)
2a=b+d....(ii)⇒b,a,d∈AP
(ii) - (i)
a−b=c+d
⇒d+e>C+d
⇒e>c
Again , c+d>a+e⇒a+b>a+e
⇒b>e
rArc<e<b
Combing , the results we can conclude :
d>a>b>e>c
|
Similar Questions
Knowledge Check
If a +b > c+d and b + c> a+d, then it is definite that
A1. c>dB2. b>dC3. a>dD4. b>cIf A+B>C+D and D+A<B+C, then
AD>BBC>DCA>DDB>D
In Figure, it is given that AB=BC and AD=EC . Prove that ABE≅CBD

View SolutionIn Figure, it is given that AE=AD and BD=CE. Prove that AEB≅ADC
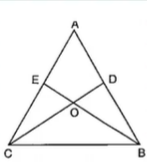
View SolutionIn Figure, it is given that AB=BC and AD=EC. Prove that abe ≅CBD (ii) BD=BE

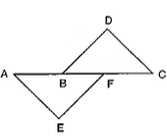
View SolutionIn Figure, it is given that AB=CF, EF=BD and ∠AFE= ∠CBD. Prove that AFE= ≅CBD
View SolutionIf a, b, c, d and e ar positive ral numbers such that
a+b+c+d+e=15and
ab2c3d4e5=(120)3(50), then the value of a2+b2+c2+d2+e2 is .................
View SolutionIf a, b, c, d, e are five consecutive odd numbers, their average is (a) 5(a+4) (b) abcde5 (c) 5(a+b+c+d+e) (d) None of these
View Solution