What should be the value of 0 if charge and velocity are constant and the final output of magnetic force should be one ?
Zero
90
180
270
The correct Answer is:B
To solve the problem, we need to determine the value of the angle θ such that the magnetic force Fm is equal to 1, given that the charge q and the velocity v are constant. The magnetic force is given by the equation:
Fm=qvBsinθ
where:
- Fm is the magnetic force,
- q is the charge,
- v is the velocity,
- B is the magnetic field strength,
- θ is the angle between the velocity vector and the magnetic field vector.
1. Set up the equation: We want the magnetic force Fm to be equal to 1. Therefore, we can write:
qvBsinθ=1
2. Assume qvB=1: For simplicity, let's assume that the product qvB=1. This simplifies our equation to:
sinθ=1
3. Determine the angle θ: The sine function equals 1 at:
θ=90∘
4. Check other options:
- If θ=0∘:
sin0∘=0⟹Fm=0(not valid)
- If θ=180∘:
sin180∘=0⟹Fm=0(not valid)
- If θ=270∘:
sin270∘=−1⟹Fm=−qvB(not valid since we want a positive force)
5. Conclusion: The only angle that satisfies the condition Fm=1 is:
θ=90∘
Thus, the value of θ should be 90∘.
- Fm is the magnetic force,
- q is the charge,
- v is the velocity,
- B is the magnetic field strength,
- θ is the angle between the velocity vector and the magnetic field vector.
qvBsinθ=1
sinθ=1
θ=90∘
- If θ=0∘:
sin0∘=0⟹Fm=0(not valid)
- If θ=180∘:
sin180∘=0⟹Fm=0(not valid)
- If θ=270∘:
sin270∘=−1⟹Fm=−qvB(not valid since we want a positive force)
θ=90∘
Similar Questions
What should be the value of K for the equillibrium condition.?
View SolutionWhat should be the value of R in figure fo which the current in it is zero?

View SolutionExplain how magnets should be stored.
View SolutionWhat should be the value of a if the value of 2x2+x−a equals to 5, when x=0 ?
View SolutionWhat should be the composition of gametes ?
View SolutionA charge Q is to be divided on two objects. What should be the values of the charges on the objects so that the force between the objects can be maximum?
View SolutionWhat should be the maximum velocity of an electron orbiting around a hydrogen nucleus
View SolutionWhat should be the maximum velocity of an electron orbiting around a hydrogen nucleus
View SolutionIn Fig. what should be the value of d so that image is formed on the object itself .
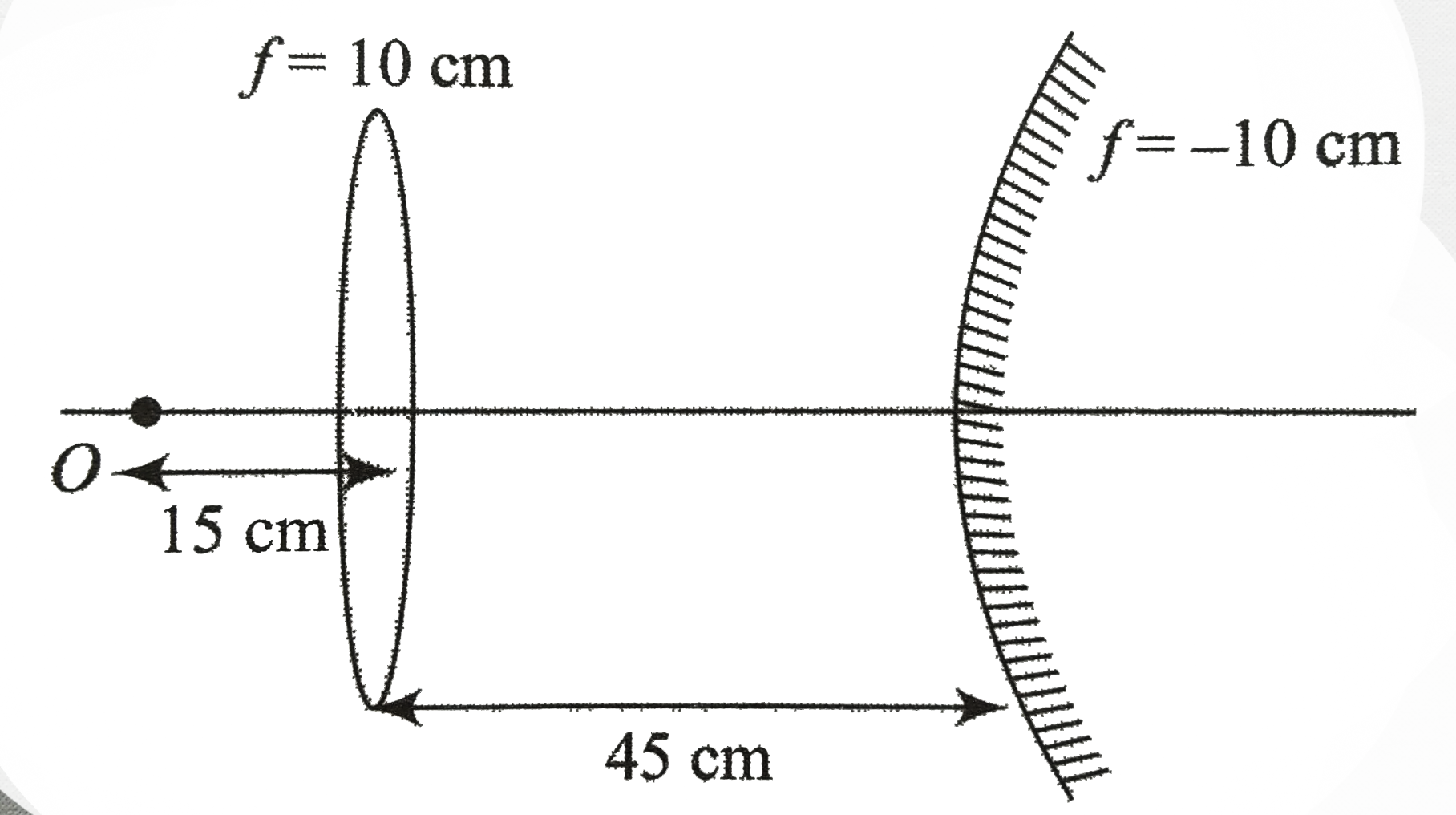
View SolutionA charge q is to be distributed on two conducting spheres. What should be the value of the charges on the spheres so that the repulsive force between them is maximum when they are placed at a fixed distance from each other in air ?
View Solution
