The magnitude of magnetic force is expressed as?
Fm=qvBsinθ
Fm=qvBcosθ
Fm=qvBtanθ
Fm=qvB/sinθ
The correct Answer is:A
To find the magnitude of the magnetic force, we can follow these steps:
1. Understanding the Magnetic Force: The magnetic force (Fm) experienced by a charged particle moving in a magnetic field is given by the equation involving the charge (q), the velocity (v), and the magnetic field (B).
2. Using the Cross Product: The magnetic force can be expressed using the vector cross product:
Fm=q(v×B)
Here, v is the velocity vector of the charged particle, and B is the magnetic field vector.
3. Magnitude of the Cross Product: The magnitude of the cross product v×B is given by:
|v×B|=|v||B|sinθ
where θ is the angle between the velocity vector and the magnetic field vector.
4. Substituting into the Force Equation: Now, substituting the magnitude of the cross product back into the force equation gives:
|Fm|=q|v||B|sinθ
5. Final Expression: Thus, the magnitude of the magnetic force can be expressed as:
Fm=qvBsinθ
6. Identifying the Correct Option: From the options given in the question, the correct expression for the magnitude of the magnetic force is:
Fm=qvBsinθ
which corresponds to option number one.
Conclusion:
The magnitude of the magnetic force is expressed as:
Fm=qvBsinθ
Fm=q(v×B)
Here, v is the velocity vector of the charged particle, and B is the magnetic field vector.
|v×B|=|v||B|sinθ
where θ is the angle between the velocity vector and the magnetic field vector.
|Fm|=q|v||B|sinθ
Fm=qvBsinθ
Fm=qvBsinθ
which corresponds to option number one.
The magnitude of the magnetic force is expressed as:
Fm=qvBsinθ
Similar Questions
A wire carrying current i is bent as shown in figure and placed in the plane of uniform magnetic field Bvec. The magnitude of magnetic force experienced by
View SolutionAssertion three infinitely long current carrying wires have equal currents and they are equally spaced. The magnitude of magnetic force on all three is same.
Reason Net force on wire-2 is zero.
View SolutionFigure shows an equilateral triangle ABC of side l carrying currents as shown, and placed in a uniform magnetic field B perpendicular to the plane of triangle. The magnitude of magnetic force on the triangle is

View SolutionFigure shows an equilateral triangle ABC of side l carrying currents as shown, and placed in a uniform magnetic field B perpendicular to the plane of triangle. The magnitude of magnetic force on the triangle is

View SolutionAn electron moving with a velocity v along the positive x-axis approaches a circular current carrying loop as shown in the fig. the magnitude of magnetic force on electron at this instant is
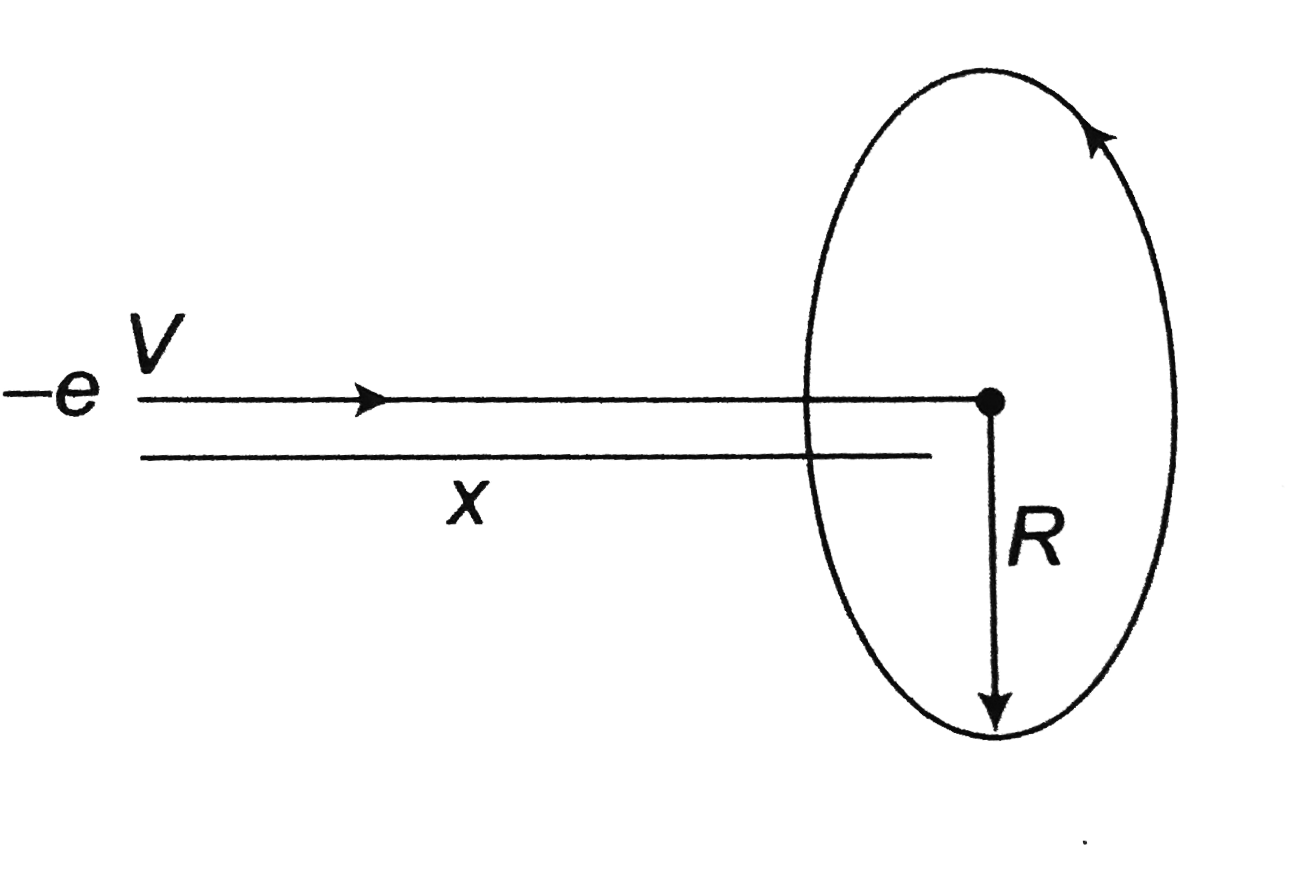
View SolutionHe2+ ion travels at right angles to a magnetic field of 0.80T with a velocity of 105ms. Find the magnitude of the magnetic force on the ion.
View SolutionWhat is the magnitude of the magnetic force per unit length on a wire carrying a current of 8 A making an angle of 30∘ with the direction of a uniform magnetic field of 0⋅15T?
View SolutionA wire of length l carries a current I along the x-asis. A magnetic field exists which is given as →B=B0(→i+→j+→k) T. find the magnitude of the magnetic force acting on the wire.
View SolutionA wire of length L carries a current i along the x-axis. A magnetic field B=B0(ˆi+ˆj+ˆk) exists in the space. Find the magnitude of the magnetic force acting on the wire.
View SolutionWhat is the magnitude of the magnetic force per unit length on a wire carrying a current of 8 A making an angle of 30∘ with the direction of a uniform magnetic field of 0⋅15T?
View Solution