What is the relationship between current density and drift velocity?
J=nevd
J=evd/n
J=n/evd
J=nvd
The correct Answer is:A
To find the relationship between current density (j) and drift velocity (vd), we can start from the fundamental definitions and equations in current electricity.
1. Understanding Current Density (j):
- Current density (j) is defined as the current (I) flowing per unit area (A) through a conductor. Mathematically, it is expressed as:
j=IA
2. Defining Drift Velocity (vd):
- Drift velocity (vd) is the average velocity that a charge carrier, such as an electron, attains due to an electric field. It is a measure of how quickly the charge carriers move through the conductor.
3. Relating Current, Charge, and Drift Velocity:
- The current (I) can also be expressed in terms of charge (Q) and time (t):
I=Qt
- For a conductor with n free charge carriers (electrons) per unit volume, the total charge (Q) that passes through a cross-sectional area in time t can be given by:
Q=n⋅A⋅vd⋅t
- Here, n is the number of charge carriers per unit volume, A is the cross-sectional area, and vd is the drift velocity.
4. Substituting into the Current Equation:
- Substituting this expression for Q into the equation for current (I):
I=n⋅A⋅vd⋅tt=n⋅A⋅vd
5. Substituting into Current Density Equation:
- Now substituting this expression for I back into the equation for current density (j):
j=IA=n⋅A⋅vdA=n⋅vd
6. Final Relationship:
- Therefore, we arrive at the relationship between current density and drift velocity:
j=n⋅e⋅vd
- Here, e is the charge of an electron. Thus, the relationship can also be expressed as:
j=n⋅e⋅vd
Conclusion:
The correct relationship between current density (j) and drift velocity (vd) is given by:
j=n⋅e⋅vd
- Current density (j) is defined as the current (I) flowing per unit area (A) through a conductor. Mathematically, it is expressed as:
j=IA
- Drift velocity (vd) is the average velocity that a charge carrier, such as an electron, attains due to an electric field. It is a measure of how quickly the charge carriers move through the conductor.
- The current (I) can also be expressed in terms of charge (Q) and time (t):
I=Qt
- For a conductor with n free charge carriers (electrons) per unit volume, the total charge (Q) that passes through a cross-sectional area in time t can be given by:
Q=n⋅A⋅vd⋅t
- Here, n is the number of charge carriers per unit volume, A is the cross-sectional area, and vd is the drift velocity.
- Substituting this expression for Q into the equation for current (I):
I=n⋅A⋅vd⋅tt=n⋅A⋅vd
- Now substituting this expression for I back into the equation for current density (j):
j=IA=n⋅A⋅vdA=n⋅vd
- Therefore, we arrive at the relationship between current density and drift velocity:
j=n⋅e⋅vd
- Here, e is the charge of an electron. Thus, the relationship can also be expressed as:
j=n⋅e⋅vd
The correct relationship between current density (j) and drift velocity (vd) is given by:
j=n⋅e⋅vd
Similar Questions
Define the term 'drift velocity' of electrons in a current carrying conductor. Obtain the relationship between the current density and the drift velocity of electrons.
View SolutionWhat is the relationship between (I) & (II)
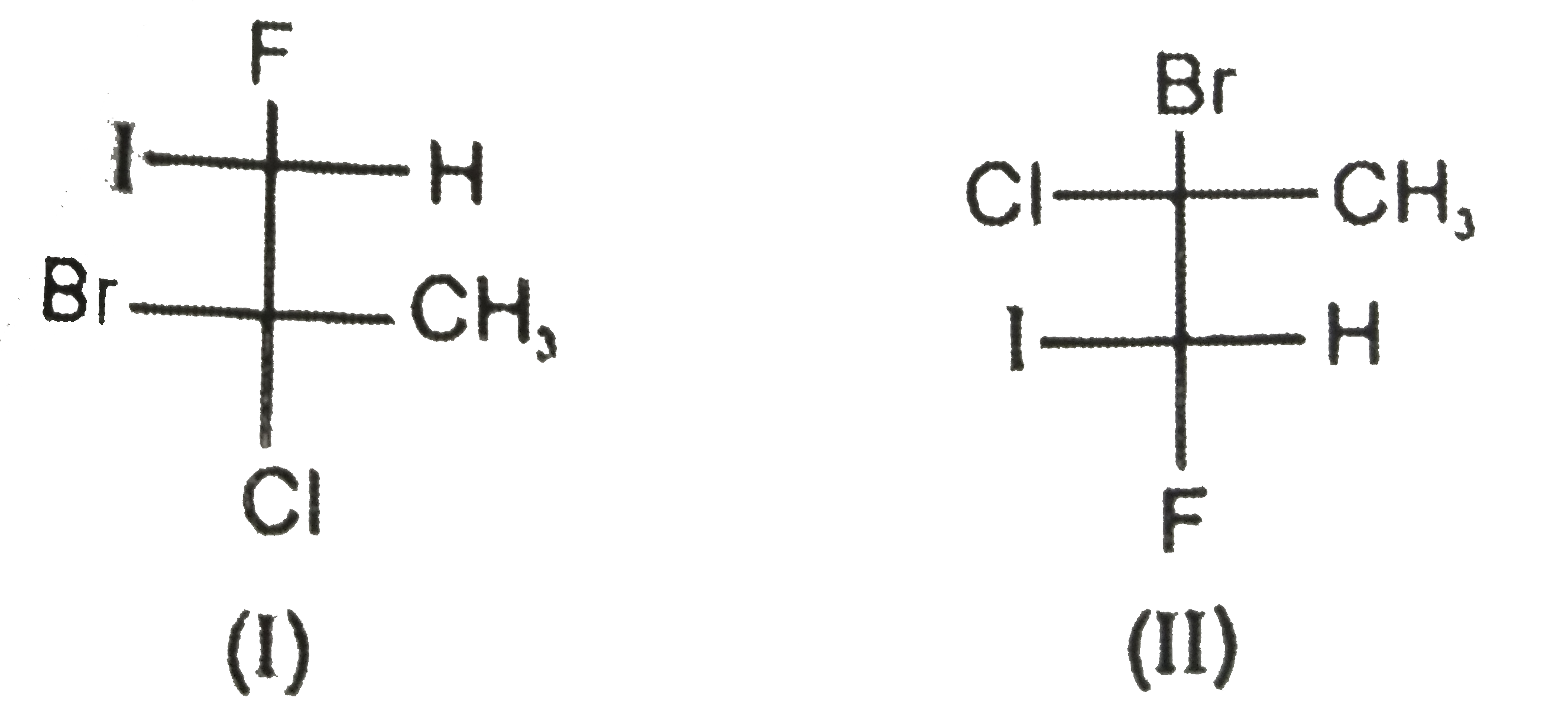
View SolutionWhat is drift velocity? Establish a relation between current and drift velocity?
View SolutionFor a metallic conductor, what is the relation between current density (J), conductivity (σ) and electric field intensity E?
View SolutionWhat is the relationship between KpandKc ?
View Solutionwhat is the relation between Mass and density.
View SolutionWhat is the relationship between the structures shown ?
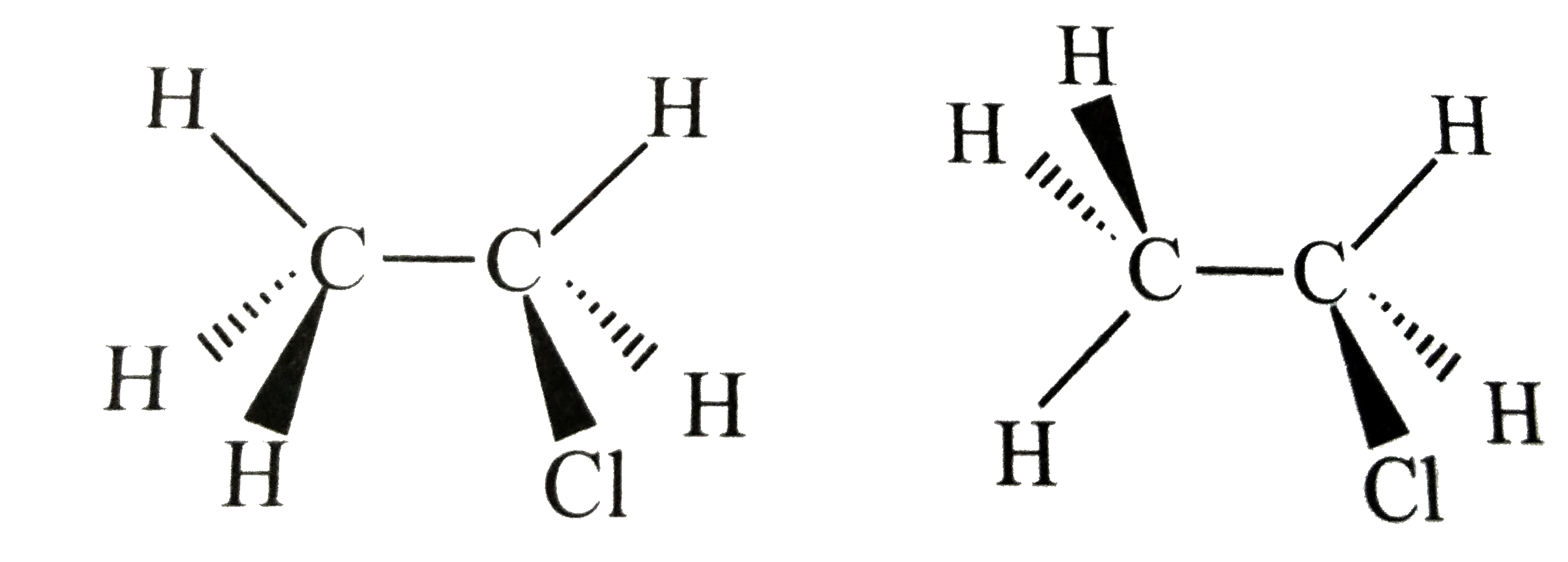
View SolutionWhat is the relationship between the structure below?
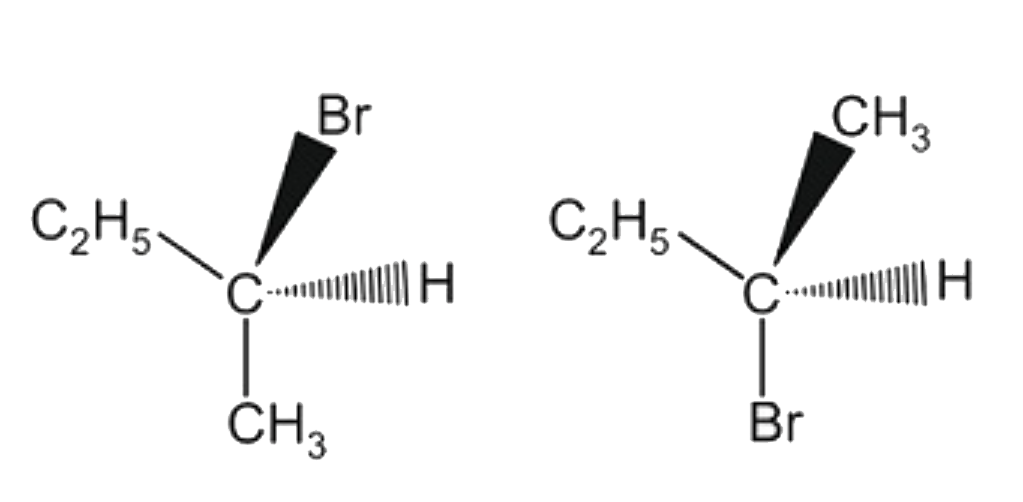
View SolutionGive the relationship between pressure and density of gas.
View SolutionWhat is the relationship between ∠AON and ∠NOB?
View Solution
