Read the following paragraph and answer the question :
The figure shows a series LCR circuit :
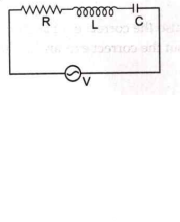 For such a circuit, the impedance Z=√R2+(XL−XC)2 , is given by where XL, and XC are inductive and capacitive resistances respectively. As the frequency of a.c. is increased, at a particular frequency. XL become, equal to XC. For that frequency maximum current occurs. This is because impedance becomes equal is its least value R. Current through the circuit I=VR. The circuit behaves like a pure resistive circuit and current and voltage will be in phase. This is called resonance. Frequency of a.c. at which resonance occurs is called resonant frequency. If frequency is less than the resonant frequency, then the capacitive reactance will be more. The circuit will be capacitive in nature and current leads voltage. On the other hand, if frequency is more than the resonant frequency inductive reactance will be more. Circuit is inductive in nature and current lags the voltage. An LCR circuit with a resistance 50Ω has a resonant angular frequency 2×103 rad/s. At resonance, the voltage across the resistance and inductance are 25 V and 20 V respectively. Then:
For such a circuit, the impedance Z=√R2+(XL−XC)2 , is given by where XL, and XC are inductive and capacitive resistances respectively. As the frequency of a.c. is increased, at a particular frequency. XL become, equal to XC. For that frequency maximum current occurs. This is because impedance becomes equal is its least value R. Current through the circuit I=VR. The circuit behaves like a pure resistive circuit and current and voltage will be in phase. This is called resonance. Frequency of a.c. at which resonance occurs is called resonant frequency. If frequency is less than the resonant frequency, then the capacitive reactance will be more. The circuit will be capacitive in nature and current leads voltage. On the other hand, if frequency is more than the resonant frequency inductive reactance will be more. Circuit is inductive in nature and current lags the voltage. An LCR circuit with a resistance 50Ω has a resonant angular frequency 2×103 rad/s. At resonance, the voltage across the resistance and inductance are 25 V and 20 V respectively. Then:
The value of inductance is :
20mH
10mH
40mH
25mH
The correct Answer is:A
Step by step video, text & image solution for Read the following paragraph and answer the question :The figure shows a series LCR circuit :For such a circuit, the impedance Z=sqrt(R^2+(X_L-X_C)^2) , is given by where X_L, and X_C are inductive and capacitive resistances respectively. As the frequency of a.c. is increased, at a particular frequency. X_L become, equal to X_C. For that frequency maximum current occurs. This is because impedance becomes equal is its least value R. Current through the circuit I= V/R. The circuit behaves like a pure resistive circuit and current and voltage will be in phase. This is called resonance. Frequency of a.c. at which resonance occurs is called resonant frequency. If frequency is less than the resonant frequency, then the capacitive reactance will be more. The circuit will be capacitive in nature and current leads voltage. On the other hand, if frequency is more than the resonant frequency inductive reactance will be more. Circuit is inductive in nature and current lags the voltage. An LCR circuit with a resistance 50 Omega has a resonant angular frequency 2 xx 10^3 rad/s. At resonance, the voltage across the resistance and inductance are 25 V and 20 V respectively. Then: The value of inductance is : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
In a R, L, C circult, three elements is connected in series by an ac source. If frequency is less than resonating frequency then net impedance of the circuit will be
AcapacitiveBinductiveCcapacitive or inductiveDpure resistiveIn series L−C−R resonant circuit, to increase the resonant frequency
AL will have to be increasedBC will have to be increasedCLC will have to be decreasedDLC will have to be increasedResonant frequency is given by (for a series L-C-R circuit)
A2π√LCB12π√LCC2π√LCD12π√LC
In a series L–C–R circuit XL,XCandR are the inductive reactance, capacitive reactance and resistance respectively at a certain frequency f. If the frequency of a.c. is doubled, what will be the values of reactances and resistance of the circuit?
View SolutionCurrent through an AC series L-C-R circuit is 2 A if operated at resonance frequency , and 1 A if operated at 50% less than resonant frequency . The current (in A) if the frequency is 100% more than the resonant frequency , is
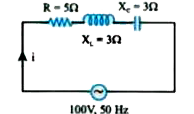
View SolutionIn a series L-C-R circuit shown in the figure , what is the resonance frequency and the current at the resonating frequency?
View SolutionThe figure shows variation of R,XL and XC with frequency f in a series L,C,R circuit. Then for what frequency point, the circuit is inductive ?
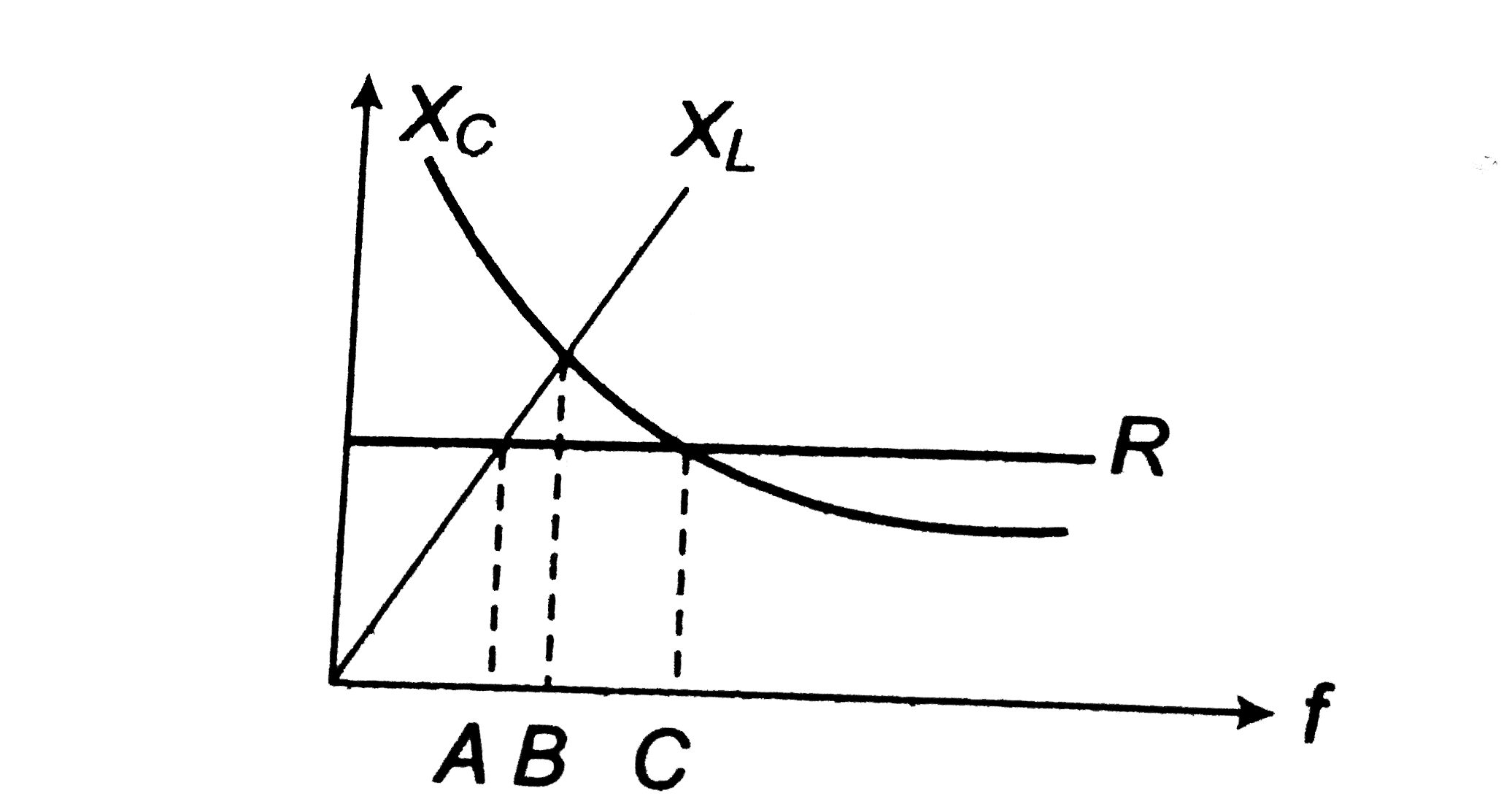
View SolutionThe natural frequency of a L - C circuit is equal to
View Solution