Q amount of electric charge is present on the surface having radius R. Then electrical potential energy of this system is :
kQR
(kQ)2R2
kQ22R
kQ22R2
The correct Answer is:C
To find the electrical potential energy of a system with charge Q distributed on the surface of a sphere with radius R, we can follow these steps:
1. Understand the System: We have a spherical surface with radius R that carries a total charge Q. This charge is uniformly distributed over the surface.
2. Identify the Capacitance: The capacitance C of a spherical capacitor (or a sphere with charge) is given by the formula:
C=4πϵ0R
where ϵ0 is the permittivity of free space.
3. Calculate the Electric Potential V: The electric potential V at the surface of the sphere due to the charge Q is given by:
V=KQR
where K is Coulomb's constant, K=14πϵ0. Thus, we can express V as:
V=Q4πϵ0R
4. Use the Formula for Potential Energy: The electrical potential energy U stored in a capacitor is given by:
U=Q22C
5. Substitute the Value of Capacitance: Substitute the expression for capacitance C into the potential energy formula:
U=Q22⋅(4πϵ0R)
6. Simplify the Expression: This simplifies to:
U=Q28πϵ0R
7. Final Result: Thus, the electrical potential energy of the system is:
U=KQ22R
where K=14πϵ0.
Final Answer:
U=KQ22R
C=4πϵ0R
where ϵ0 is the permittivity of free space.
V=KQR
where K is Coulomb's constant, K=14πϵ0. Thus, we can express V as:
V=Q4πϵ0R
U=Q22C
U=Q22⋅(4πϵ0R)
U=Q28πϵ0R
U=KQ22R
where K=14πϵ0.
U=KQ22R
Similar Questions
Knowledge Check
Two point charges 2q and 8q are placed at a distance r apart. Where should a third charge −q be placed between them so that the electrical potential energy of the system is a minimum
Aat a distance of r/3 from 2qBat a distance of 2r/3 from 2qCat a distance of r/16 from 2qDNone of the aboveTwo positive point charges are separated by a distance R. If the distance between the charges is reduced to R/2, what happens to the total electric potential energy of the system?
AIt is doubledBIt is reduced to one-half of its original valueCIt remains the sameDIt is reduced to one-fourth of its original valueWhen the separation between two charges is increase the electric potential energy of the charges.
AincreasesBdecreasesCremains the same.Dmay increase or decrease
Three charges are placed as shown in fig if the electric potential energy of system is zero, then Q : q-
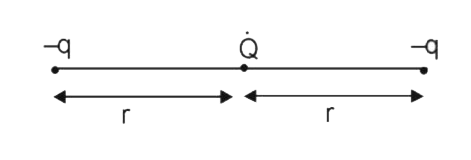
View SolutionThree point charges +q, +2q and Q are placed at the three vertices of an equilateral triangle. Find the value of charge Q (in terms of q), so that electric potential energy of the system is zero.
View SolutionFind the electric potential energy of a uniformly charged sphere.
View SolutionElectric charges q,q,2q are placed at the equilateral triangle ABC of side l .The electric dipole moment of the system is ?
View SolutionTwo point charge qA and qB are placed in a uniform external electric field →E at point A and B respectively. The position vector of A is →rA and that of B is →rB. if V(→rA) and V(→rB) be the electric potentials at point A and B due to the external electric field →E, then potential energy of the system will be
View Solution
