Lorentz force is :
the vector sum of electrostatic and magnetic force acting on a moving charged particle .
the vector sum of gravitational and magnetic force acting on a moving charged particle.
electrostatic force acting on a charged particle
magnetic force acting on a moving charged particle.
The correct Answer is:A
To solve the question regarding the Lorentz force, we need to understand its definition and the components that contribute to it.
1. Understanding the Lorentz Force: The Lorentz force is the total force experienced by a charged particle moving in electric and magnetic fields. It combines the effects of both fields.
2. Components of the Lorentz Force:
- The force due to the electric field (→E) is given by:
→FE=q→E
where q is the charge of the particle.
- The force due to the magnetic field (→B) is given by:
→FB=q(→v×→B)
where →v is the velocity of the charged particle and × denotes the cross product.
3. Combining the Forces: The total Lorentz force (→F) acting on the charged particle is the vector sum of the electric and magnetic forces:
→F=→FE+→FB=q→E+q(→v×→B)
4. Identifying the Correct Option: From the options provided:
- Option 1 states that the Lorentz force is the vector sum of the electrostatic and magnetic force acting on a moving charged particle. This is consistent with our derived expression for the Lorentz force.
- Other options either mention gravitational force or only one of the forces (electrostatic or magnetic), which do not encapsulate the complete definition of the Lorentz force.
5. Conclusion: Therefore, the correct answer is:
The Lorentz force is the vector sum of electrostatic and magnetic force acting on a moving charged particle.
Final Answer:
The correct option is Option 1.
---
- The force due to the electric field (→E) is given by:
→FE=q→E
where q is the charge of the particle.
- The force due to the magnetic field (→B) is given by:
→FB=q(→v×→B)
where →v is the velocity of the charged particle and × denotes the cross product.
→F=→FE+→FB=q→E+q(→v×→B)
- Option 1 states that the Lorentz force is the vector sum of the electrostatic and magnetic force acting on a moving charged particle. This is consistent with our derived expression for the Lorentz force.
- Other options either mention gravitational force or only one of the forces (electrostatic or magnetic), which do not encapsulate the complete definition of the Lorentz force.
The Lorentz force is the vector sum of electrostatic and magnetic force acting on a moving charged particle.
The correct option is Option 1.
Similar Questions
State the Biot-Savart law which gives the magnetic field B at a distance r from a current element. Hence obtain an expression for the magnetic field BQ due to a point charge Q moving with constant velocity v (assumed non-relativistic).
Point charge Q and Q' are constrained to move along the x-and y-axes, respectively, with the same uniform speed v. AT time t = 0 both charges are at the origin. At time t calculate the Lorentz force F on Q' due to the magnetic field of Q
View SolutionA long straight copper wire, of circular cross ection, contains n conduction electrons per unit volume, each of charge q. Show that the current l in the wire is given by
l=nqvπa2
where v is the drift velocity and a is the radius of the wire.
At a radial distance r from the axis of the wire, what is the direction of the magnetic field B due to the current l? Assuming that the magnitude of the field is B=μ0l/2πr(r≥a), obtain an expression for the Lorentz force F on an electron moving with the drift velocity at the surface of the wire.
If l=10 A and a = 0.5mm, calcualte the magnitude of (a) the drift velocity and (b) the forcce, given that for copper, n=8.5×1028m−3
View Solution
Knowledge Check
A particle of charged 1μC is at rest in a magnetic field →B=−2ˆk tesla. Magnetic Lorentz force on the charge particle with respect to an observer moving with velocity →v=−6ˆims−1 will be
AZeroB−105ˆjNC−106ˆJD+10−5ˆjNA proton is moving with a velocity of 5×105m/s along the Y-direction. It is acted upon by an electric field of intensity 105 V/m along the X-direction and a magnetic field of 1Wb/m2 along the Z-direction. Then the Lorentz force on the particle is :
AzeroB8.0×10−4 N along X-axisC9.6×10−14 along Z-axisD9.6×10−14 along X-axis
A charged particle is moving in a circular path under the action of the Lorentz force. How much work is done by the force in one revolution?
View SolutionA charged particle is moving on a circular path of radius R in a uniform magnetic field under the Lorentz force F. How much work is done by the force in one round? Is the momentum of the particle changing?
View SolutionIf the magnetic field is parallel to the positive y-axis and the charged particle is moving along the positive x-axis (Fig.), which way would the Lorentz force be for (a) an electron (negative charge), (b) a proton (positive charge).
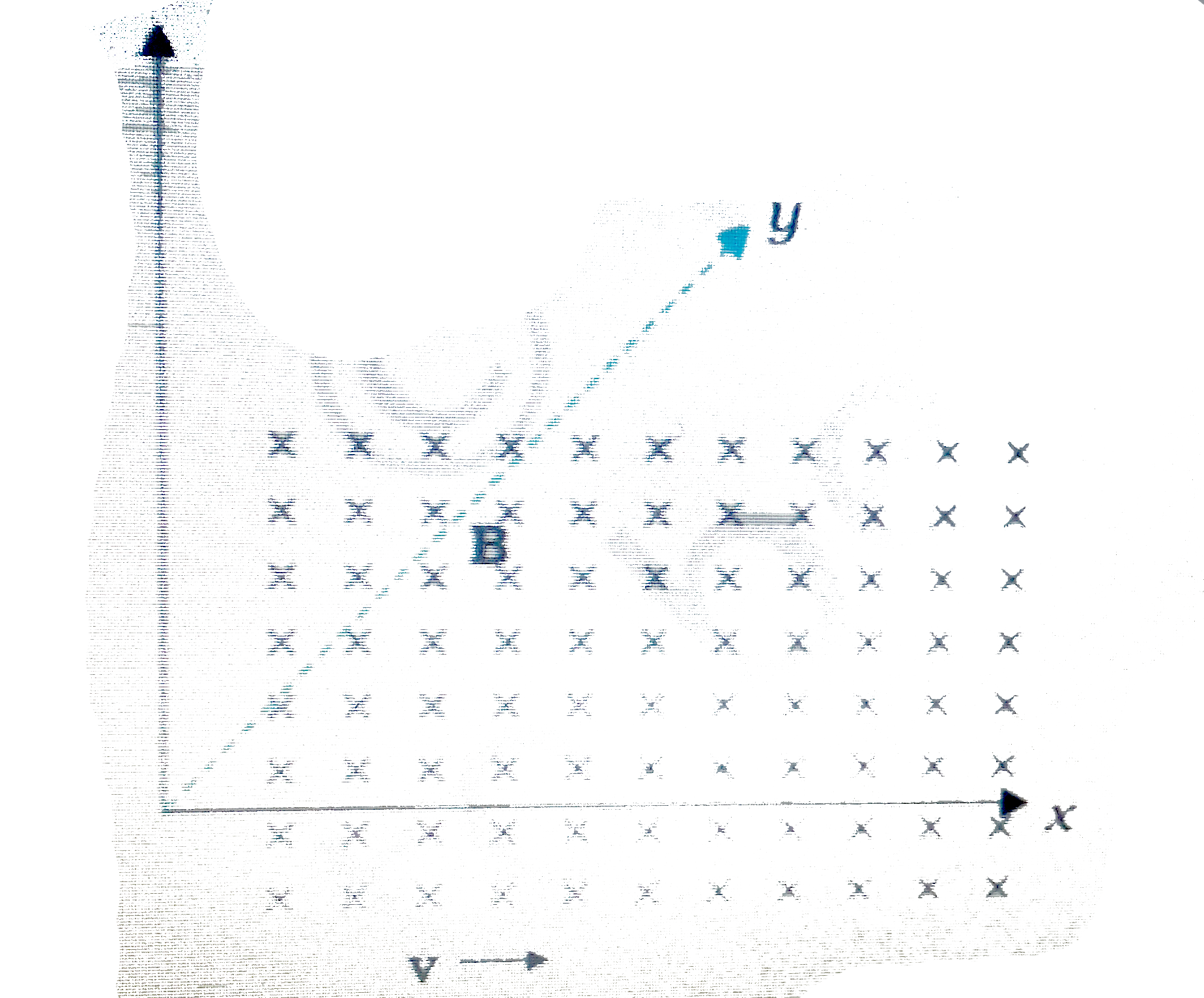
View SolutionIf the magnetic field is parallel to the positive y-axis and the charged particle is moving along the positive x-axis (Fig.), which way would the Lorentz force be for (a) an electron (negative charge), (b) a proton (positive charge).
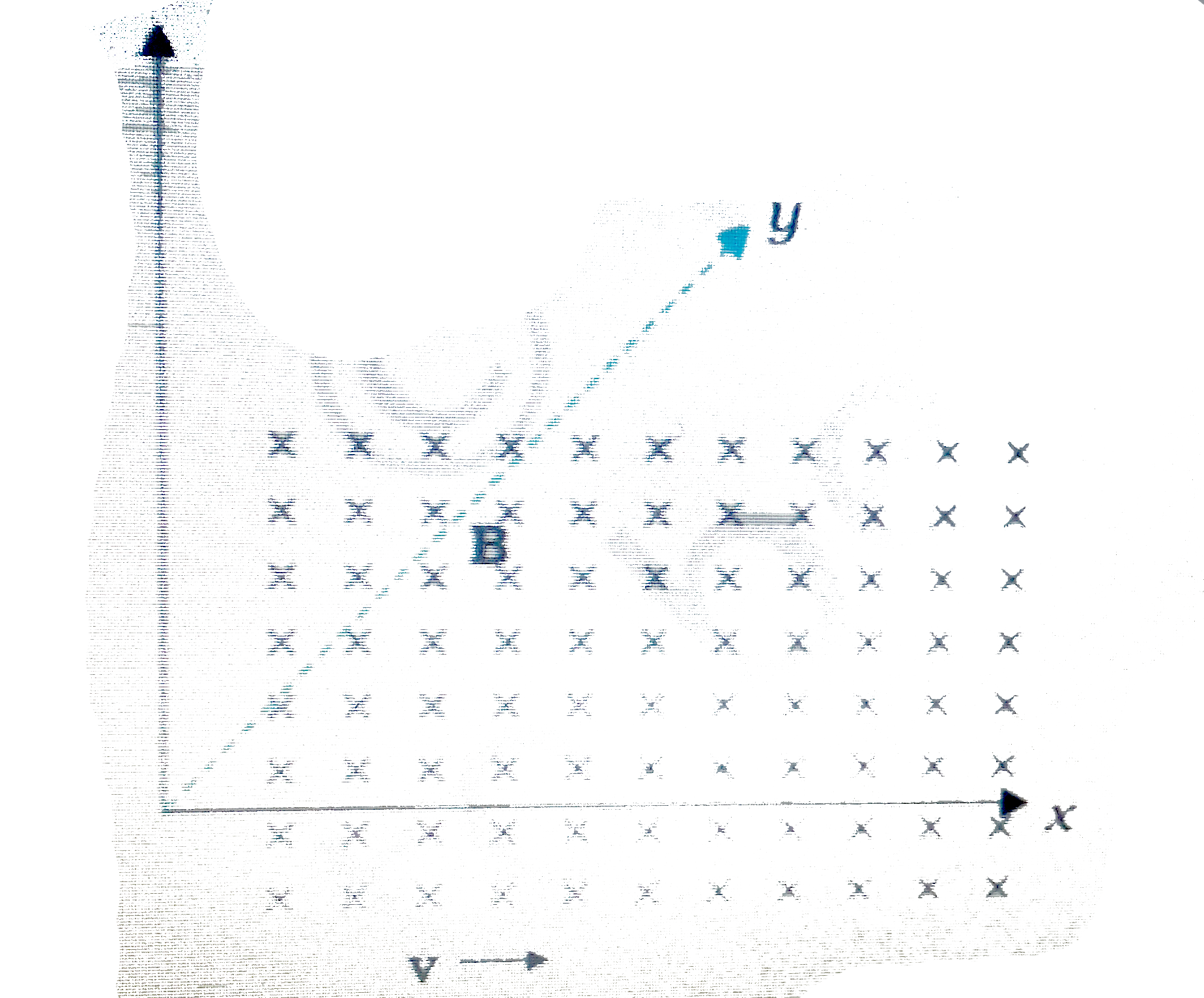
View SolutionStatement - 1 : For a charged particle to pass through a uniform electro-magnetic field without change in velocity, its velocity vector must be perpendicular to the magnetic field. Statement - 2 : Net Lorentz force on the particle is given by →F=q[→E+→v×→B].
View SolutionA charge particle having charge 2 coulomb is thrown with velocity 2ˆi+3ˆj inside a region having →E=2ˆj and magnetic field 5ˆk. Find the initial Lorentz force acting on the particle
View Solution