A charged particle moving in a magnetic field experiences a resultant force :
In the direction perpendicular to both the field and its velocity .
in the direction of the field.
in the direction opposite to that of the field.
None of the above
The correct Answer is:A
To solve the problem of determining the direction of the resultant force experienced by a charged particle moving in a magnetic field, we can follow these steps:
1. Understanding the Scenario:
- We have a charged particle (let's say a positive charge, +q) moving in a magnetic field (B). The magnetic field is uniform and directed perpendicularly to the plane of motion of the charged particle.
2. Identifying the Directions:
- Assume the velocity (v) of the charged particle is along the positive x-axis.
- The magnetic field (B) is directed into the plane, which we can denote as the negative z-axis.
3. Applying the Lorentz Force Law:
- The force (F) experienced by a charged particle moving in a magnetic field is given by the Lorentz force equation:
F=q(v×B)
- Here, × denotes the cross product.
4. Determining the Magnitude and Direction of the Force:
- The magnitude of the force can be expressed as:
F=qvBsin(θ)
- In our case, since the velocity (v) and the magnetic field (B) are perpendicular to each other, θ=90∘ and sin(90∘)=1. Therefore, the force simplifies to:
F=qvB
5. Using the Right-Hand Rule:
- To find the direction of the force, we use the right-hand rule:
- Point your right thumb in the direction of the velocity (v).
- Curl your fingers in the direction of the magnetic field (B).
- Your palm will then point in the direction of the force (F).
- In this case, with v along the positive x-axis and B into the page (negative z-axis), the force will be directed upwards (positive y-axis).
6. Conclusion:
- The resultant force on the charged particle is perpendicular to both the velocity and the magnetic field. Therefore, the correct answer is that the force is in the direction perpendicular to both the field and its velocity.
Final Answer:
The resultant force experienced by the charged particle is in the direction perpendicular to both the magnetic field and its velocity (Option 1).
- We have a charged particle (let's say a positive charge, +q) moving in a magnetic field (B). The magnetic field is uniform and directed perpendicularly to the plane of motion of the charged particle.
- Assume the velocity (v) of the charged particle is along the positive x-axis.
- The magnetic field (B) is directed into the plane, which we can denote as the negative z-axis.
- The force (F) experienced by a charged particle moving in a magnetic field is given by the Lorentz force equation:
F=q(v×B)
- Here, × denotes the cross product.
- The magnitude of the force can be expressed as:
F=qvBsin(θ)
- In our case, since the velocity (v) and the magnetic field (B) are perpendicular to each other, θ=90∘ and sin(90∘)=1. Therefore, the force simplifies to:
F=qvB
- To find the direction of the force, we use the right-hand rule:
- Point your right thumb in the direction of the velocity (v).
- Curl your fingers in the direction of the magnetic field (B).
- Your palm will then point in the direction of the force (F).
- In this case, with v along the positive x-axis and B into the page (negative z-axis), the force will be directed upwards (positive y-axis).
- The resultant force on the charged particle is perpendicular to both the velocity and the magnetic field. Therefore, the correct answer is that the force is in the direction perpendicular to both the field and its velocity.
The resultant force experienced by the charged particle is in the direction perpendicular to both the magnetic field and its velocity (Option 1).
Similar Questions
Knowledge Check
A charged particle is moving along a magnetic field line. The magnetic force on the particle is
Aalong its velocityBopposite to its velocityCperpendicular to its velocityDzeroA charged particle moving in a unifrom magnetic experiences a force of maximum magnitude when direction of motion of charged particle is .
Aparallel to the direction of magnetic fieldBat right angle to the direction of magnetic fieldCantiparallel to the direction of magnetic fieldDinclined at 45∘ to the direction of magnetic field .A charged particle is moving in a magnetic field of strength B perpendicular to the direction of the field. If q and m denote the charge and mass of the particle respectively, then the frequency of rotation of the particle is
AqB2πmBqB2πm2C2π2mqBD2πmqB
Moving charges in a magnetic field would experience a force.
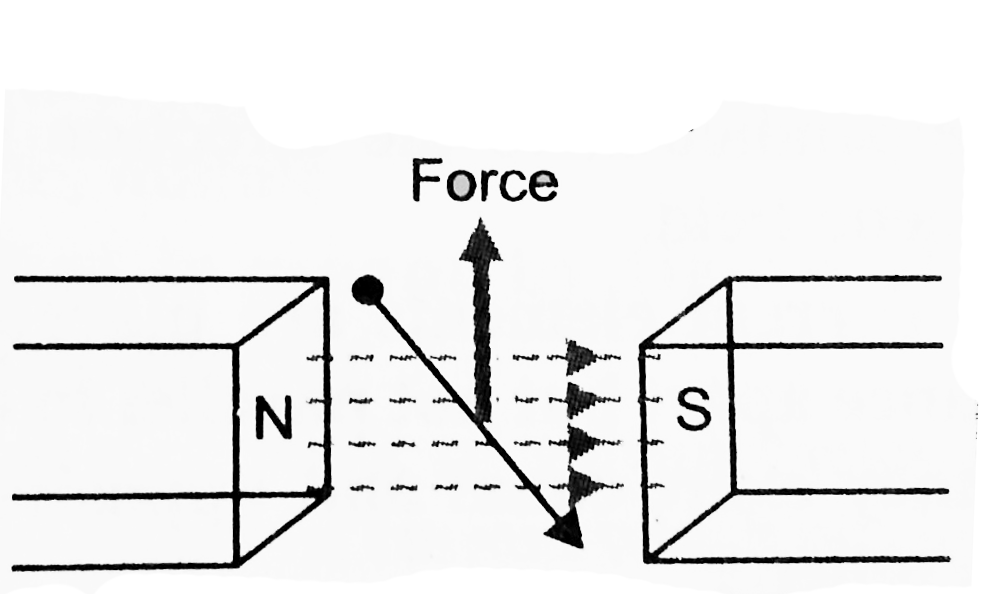
View SolutionA charged particle enters into a uniform magnetic field and experiences upward force as indicated in figure. What is the charge sign on the particle?
View SolutionA charged particle is moved along a magnetic field line. The magnetic force on the particle is
View SolutionAssertion (A): An alpha particle placed in a magnetic field will not experience any force, if it moves in the magnetic field parallel to field lines.
Reason (R): The force is zero if current and field are in the same direction.
View SolutionA charged particle is moving with velocity Vin magnetic field
View Solution
