How does the current in an RC circuit vary when the charge on the capacitor build up ?
It decreases linearly
It increases linearly
it decreases exponentially
It increases exponentially
The correct Answer is:C
To understand how the current in an RC circuit varies when the charge on the capacitor builds up, we can analyze the charging process of the capacitor step by step.
1. Understanding the RC Circuit:
- An RC circuit consists of a resistor (R) and a capacitor (C) connected in series with a voltage source (V). Initially, when the switch is closed, the capacitor is uncharged.
2. Initial Condition (T = 0):
- At time T=0, the capacitor has no charge. When the switch is closed, the capacitor behaves like a short circuit (it offers zero resistance), allowing maximum current to flow through the circuit.
- The maximum current I0 can be calculated using Ohm's Law:
I0=VR
3. Charging Process:
- As time progresses, the capacitor begins to charge. The charge Q on the capacitor increases over time.
- The relationship between the charge Q on the capacitor and the voltage across it is given by:
Q=C⋅VC
- Here, VC is the voltage across the capacitor.
4. Current Decay:
- The current I in the circuit is related to the rate of change of charge on the capacitor:
I=−dQdt
- As the capacitor charges, the rate of change of charge decreases, leading to a decrease in current.
5. Exponential Decay of Current:
- The current in the RC circuit during charging follows an exponential decay function:
I(t)=I0e−tRC
- This equation shows that the current decreases exponentially over time as the capacitor charges.
6. Final Condition (T → ∞):
- As time approaches infinity, the capacitor becomes fully charged, and the current in the circuit approaches zero:
I(t→∞)=0
- At this point, the capacitor behaves like an open circuit, preventing any current from flowing.
Conclusion:
- The current in an RC circuit decreases exponentially as the charge on the capacitor builds up. Therefore, the correct answer to the question is that the current decreases exponentially.
- An RC circuit consists of a resistor (R) and a capacitor (C) connected in series with a voltage source (V). Initially, when the switch is closed, the capacitor is uncharged.
- At time T=0, the capacitor has no charge. When the switch is closed, the capacitor behaves like a short circuit (it offers zero resistance), allowing maximum current to flow through the circuit.
- The maximum current I0 can be calculated using Ohm's Law:
I0=VR
- As time progresses, the capacitor begins to charge. The charge Q on the capacitor increases over time.
- The relationship between the charge Q on the capacitor and the voltage across it is given by:
Q=C⋅VC
- Here, VC is the voltage across the capacitor.
- The current I in the circuit is related to the rate of change of charge on the capacitor:
I=−dQdt
- As the capacitor charges, the rate of change of charge decreases, leading to a decrease in current.
- The current in the RC circuit during charging follows an exponential decay function:
I(t)=I0e−tRC
- This equation shows that the current decreases exponentially over time as the capacitor charges.
- As time approaches infinity, the capacitor becomes fully charged, and the current in the circuit approaches zero:
I(t→∞)=0
- At this point, the capacitor behaves like an open circuit, preventing any current from flowing.
- The current in an RC circuit decreases exponentially as the charge on the capacitor builds up. Therefore, the correct answer to the question is that the current decreases exponentially.
Similar Questions
Knowledge Check
A capacitor of capacitance C is given charge Q and then connected in parallel to a coil of inductance L. There is no resitance in the circuit. When the charge on the capacitor becomes zero, the current in the coil will be
AQ√LCBQ√LCCQ√CLDzeroDisplacement current exists between the plates of capacitor , when charge of the capacitor
AConstantBMaximumCChangingDBoth (1) &(3)The conduction current in ideal case through a circuit is zero when charge on capacitor is
AzeroBmaximumCany transient valueDdepends on capacitor used
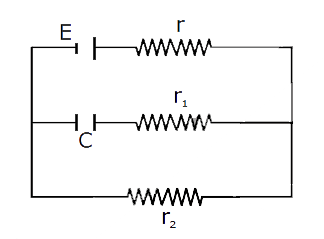
In the given circuit diagram when the current reaches steady state in the circuit , the charge on the capacitor of capacitance C will be :
View SolutionAfter switch is closed in the LC circuit shown in the figure, the charge on the capacitor is sometimes zero, but at such instants the current in the circuit is not zero. How is this behaviour possible ?

View SolutionIn circuit shown in figure charge on capacitor is Q=100μC. If switch is closed at t=0 find current in circuit when charge on capacitor reduces to 50μC. Also find the maximum current in circuit.

View SolutionA : The displacement current goes through the gap between the plates of a capacitor when the charge on the capacitor does not change.
R : Displacement current arises only when the electric field is constant.
View SolutionEnergy can be stored by an LC circuit oscillating at its natural frequency. Energy stored in a capacitor is in form of electric field between the plates. An inductor stores energy in form of magnetic field. If the inductor connected across capacitor, the voltage across the capacitor will drive the current through inductor, building up a magnetic field around it. The voltage across the capacitor falls to zero as the charge is used up by the current flow. Now the energy stored in the coil's magnetic field induces a voltage across the coil, because inductor opposes the current change. Thus energy required to charge the capacitor is extracted from the magnetic field.
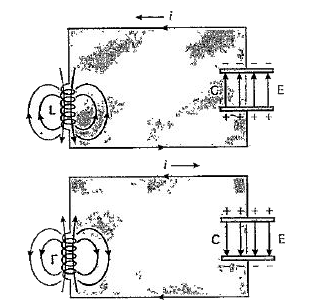
A capacitor of 25μF and inductor of 0.6 H are in an LC circuit. When the charge on capacitor is3×10−5C, what is the rate of change of current:
View Solution
