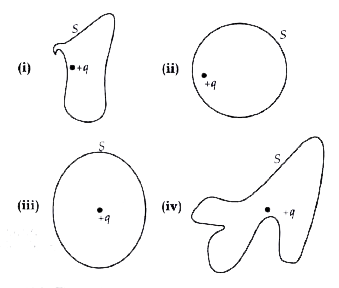If the net electric flux through a closed surface is zero, then we can infer :
no net charge is enclosed by the surface
uniform electric field exists within the surface
electric potential varies from point to point inside the surface
charge is present inside the surface
The correct Answer is:A
To solve the question, "If the net electric flux through a closed surface is zero, then we can infer:", we will analyze the implications of having zero net electric flux through a closed surface based on Gauss's Law.
1. Understanding Electric Flux:
Electric flux (Φ) through a surface is defined as the product of the electric field (E) and the area (A) through which the field lines pass, taking into account the angle (θ) between the electric field and the normal to the surface. Mathematically, it is given by:
Φ=E⋅A⋅cos(θ)
2. Applying Gauss's Law:
According to Gauss's Law, the net electric flux through a closed surface is proportional to the net charge (Q) enclosed within that surface:
Φ=Qencε0
where ε0 is the permittivity of free space.
3. Analyzing Zero Electric Flux:
If the net electric flux through the closed surface is zero (Φ = 0), applying Gauss's Law gives:
0=Qencε0
This implies that the net charge enclosed by the surface Qenc must be zero:
Qenc=0
4. Conclusion:
From the above analysis, we can conclude that if the net electric flux through a closed surface is zero, it indicates that there is no net charge enclosed by that surface. Therefore, the correct inference is:
- No net charge is enclosed by the surface.
Evaluation of Other Options:
- Option 2: "Uniform electric field exists within the surface" - This is incorrect because a uniform electric field would typically result in a non-zero flux unless the surface is oriented in such a way that the field lines enter and exit equally.
- Option 3: "Electric potential varies from point to point inside the surface" - This is also incorrect, as a conductor in electrostatic equilibrium would have a constant potential if there were no net charge inside.
- Option 4: "Charge is present inside the surface" - This is incorrect because if there were any charge present, the net flux could not be zero.
Final Answer:
The correct inference is:
- No net charge is enclosed by the surface.
Electric flux (Φ) through a surface is defined as the product of the electric field (E) and the area (A) through which the field lines pass, taking into account the angle (θ) between the electric field and the normal to the surface. Mathematically, it is given by:
Φ=E⋅A⋅cos(θ)
According to Gauss's Law, the net electric flux through a closed surface is proportional to the net charge (Q) enclosed within that surface:
Φ=Qencε0
where ε0 is the permittivity of free space.
If the net electric flux through the closed surface is zero (Φ = 0), applying Gauss's Law gives:
0=Qencε0
This implies that the net charge enclosed by the surface Qenc must be zero:
Qenc=0
From the above analysis, we can conclude that if the net electric flux through a closed surface is zero, it indicates that there is no net charge enclosed by that surface. Therefore, the correct inference is:
- No net charge is enclosed by the surface.
- Option 2: "Uniform electric field exists within the surface" - This is incorrect because a uniform electric field would typically result in a non-zero flux unless the surface is oriented in such a way that the field lines enter and exit equally.
- Option 3: "Electric potential varies from point to point inside the surface" - This is also incorrect, as a conductor in electrostatic equilibrium would have a constant potential if there were no net charge inside.
The correct inference is:
- No net charge is enclosed by the surface.
Similar Questions
Knowledge Check
If the net electric field flux passing through a closed surface is zero, then the electric field at the surface will be
A0Bsame at all placesCdepends upon the location of pointsDinfiniteThe electric flux through the surface
 Ain fig, (iv) is the largestBin fig, (iii) is the leastCin fig (ii) is same as a fig (iii) but is smaller than that in Fig (iv).Dis the same for all the figures.
Ain fig, (iv) is the largestBin fig, (iii) is the leastCin fig (ii) is same as a fig (iii) but is smaller than that in Fig (iv).Dis the same for all the figures.The electric flux through the surface
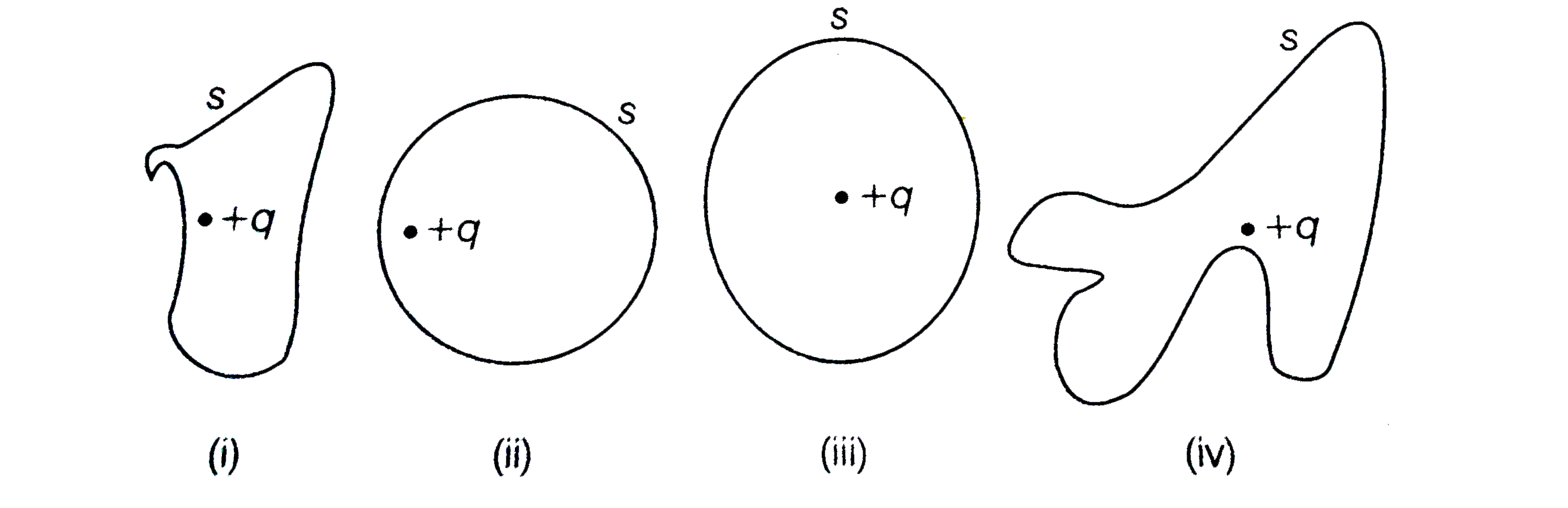 Ain fig. (iv) is the largestBin fig. (iii) is the leastCin fig. (ii) is same as fig.(iii) but is smaller than fig.(iv)DIs the same for all the figures.
Ain fig. (iv) is the largestBin fig. (iii) is the leastCin fig. (ii) is same as fig.(iii) but is smaller than fig.(iv)DIs the same for all the figures.
If the flux of the electric field through a closed surface is zero,
View SolutionIf the flux of the electric field through a closed surface is zero ,
(i) the electric field must be zero everywhere on the surface
(ii) the electric field may be zero everywhere on the surface
(iii) the charge inside the surface must be zero
(iv) the charge in the vicinity of the surface must be zero
View SolutionThe electric flux through a closed Gaussian surface depends upon
View SolutionA capacitor of capacitance C is charged to a potential V. The flux of the electric field through a closed surface enclosing the capacitor is
View SolutionWhich of the following law gives a relation between the electric flux through any closed surface and the charge enclosed by the surface ?
View Solution