In which condition an electron will move undeflected in the presence of crossed electric and magnetic field ?
When electric and magnetic field in parallel
When Electric and magnetic field in perpendicular
Both (a) and (b)
None of them
The correct Answer is:B
To determine the condition under which an electron moves undeflected in the presence of crossed electric and magnetic fields, we can follow these steps:
1. Understanding Forces on a Charged Particle:
When a charged particle, such as an electron, moves through an electric field (E) and a magnetic field (B), it experiences two forces: the electric force (F_E) and the magnetic force (F_B).
2. Electric Force Calculation:
The electric force acting on the electron is given by:
FE=qE
where q is the charge of the electron (which is negative) and E is the electric field strength.
3. Magnetic Force Calculation:
The magnetic force acting on the electron is given by the Lorentz force equation:
FB=q(v×B)
where v is the velocity of the electron and B is the magnetic field.
4. Condition for No Deflection:
For the electron to move undeflected, the net force acting on it must be zero. This means that the electric force must be equal in magnitude and opposite in direction to the magnetic force:
FE+FB=0⇒FE=−FB
5. Substituting Forces:
Substituting the expressions for the forces gives:
qE=−q(v×B)
Since q is negative (for an electron), we can simplify this to:
E=v×B
6. Direction of Fields:
The electric field (E) and the magnetic field (B) must be perpendicular to each other for the cross product v×B to yield a force that can balance the electric force. Thus, the condition for the electron to be undeflected is that the electric field and magnetic field are perpendicular to each other.
7. Conclusion:
Therefore, the condition under which an electron will move undeflected in the presence of crossed electric and magnetic fields is when the electric field and magnetic field are perpendicular to each other.
Final Answer:
The electron will move undeflected when the electric field and magnetic field are perpendicular to each other.
---
When a charged particle, such as an electron, moves through an electric field (E) and a magnetic field (B), it experiences two forces: the electric force (F_E) and the magnetic force (F_B).
The electric force acting on the electron is given by:
FE=qE
where q is the charge of the electron (which is negative) and E is the electric field strength.
The magnetic force acting on the electron is given by the Lorentz force equation:
FB=q(v×B)
where v is the velocity of the electron and B is the magnetic field.
For the electron to move undeflected, the net force acting on it must be zero. This means that the electric force must be equal in magnitude and opposite in direction to the magnetic force:
FE+FB=0⇒FE=−FB
Substituting the expressions for the forces gives:
qE=−q(v×B)
Since q is negative (for an electron), we can simplify this to:
E=v×B
The electric field (E) and the magnetic field (B) must be perpendicular to each other for the cross product v×B to yield a force that can balance the electric force. Thus, the condition for the electron to be undeflected is that the electric field and magnetic field are perpendicular to each other.
Therefore, the condition under which an electron will move undeflected in the presence of crossed electric and magnetic fields is when the electric field and magnetic field are perpendicular to each other.
The electron will move undeflected when the electric field and magnetic field are perpendicular to each other.
Similar Questions
Write the condition under which an electron will move undeflected in the presence of crossed electric and magnetic fields.
View SolutionA charged particle moving with a uniform velocity →v enters a region where uniform electric and magnetic fields →E and →B are present. It passes through the region without any change in its velocity. What can we conclude about the (i) relative direction of →E, →V and →B? (ii) magnetic of →E and →B?
or
Find the condition under which the charged particle moving with different speeds in the presence of electric and magnetic field vectors can be used to select charged particles of a particular speeds.
View Solution
Knowledge Check
In a Thomson set-up for the demination of e/m, electrons accelerated by 2.5 kV enter the region of crossed electric and magnetic fields of strengths 3.6×104Vm−1and1.2×10−3T respectively and through undeflected. The meaured value of e/m of the electron is equal to
A1.0×1011C−kg−1B1.76×1011C−kg−1C1.80×1011C−kg−1D1.85×1011C−kg−1A charged particle moves undeflected in a region of crossed electric and magnetic fields. If the electric field is switched off, the particle has an initial acceleration a. If the magnetic field is switched off, instead of electric field, the particle will have an initial acceleration
Aequal to 0B>aCequal to aD<aA charged paricle goes undeflected in a region containing electric and magnetic field. It is possible that
A¯¯¯V| |¯¯¯B and ¯¯¯E is not parallel to berBB¯¯¯E| |¯¯¯B but berV is not parallel to ¯¯¯EC¯¯¯E| |¯¯¯B ,¯¯¯V| |¯¯¯ED¯¯¯E| |¯¯¯B ,¯¯¯V⊥¯¯¯E
Find the condition under which the charged particles moving with different speeds in the presence of electric and magnetic field vectors can be used to select charged particles of a particular speed.
View SolutionA particle of charge q is moving with velocity v in the presence of crossed Electric field E and Magnetic field B as shown. Write the condition under which the particle will continue moving along x- axis. How would the trajectory of the particle be affected if the electric field is switched off?
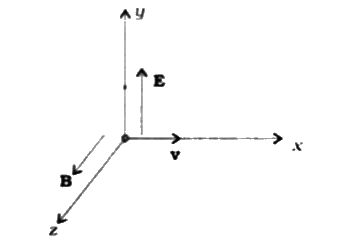
View SolutionA charged paricle goes undeflected in a region containing electric and magnetic field. It is possible that
View SolutionWrite the expression for the force →F acting on a charged particle of charge q moving with a velocity →v in the presence of both electric field →E and magnetic field →B . Obtain the condition under which the particle moves underflected through the fields.
View SolutionWrite the expression for the force →F, acting on a charged particle of charge q moving with a velocity →v in the pressure of both electric field →E and magnetic field →B. Obtain the condition under which the particle moves undeflected through the fields.
View Solution
