एक समतलोत्तल लेन्स जिसकी दोनों त्रिज्याएँ 20 सेमी हैं, एक समतल दर्पण पर रखा गया है। जब एक पिन लेन्स के 30 सेमी ऊपर लगाया जाता है तो पिन और उसके प्रतिबिम्ब के बीच लम्बन (parallax) दूर हो जाता है। अब यदि लेन्स और दर्पण के बीच एक पारदशी द्रव डाला जाए तो लम्बन को दूर करने के लिए पिन को लेन्स से 50 सेमी ऊपर रखना पड़ता है। द्रव के लेन्स की फोकस दूरी व प्रकृति बताइए तथा द्रव के अपवर्तनांक का परिकलन कीजिए।
माना उत्तल लेन्स की फोकस दूरी fg है।
चूँकि पिन का प्रतिबिम्ब वापस पिन पर ही बनता है, इसका अर्थ है कि पिन से चलने वाली किरणें लेन्स से अपवर्तन के पश्चात् समतल दर्पण पर अभिलम्बवत् गिरती हैं (दर्पण की अनुपस्थिति में अनन्त पर मिलती) और अपने मार्ग पर वापस लौट जाती हैं
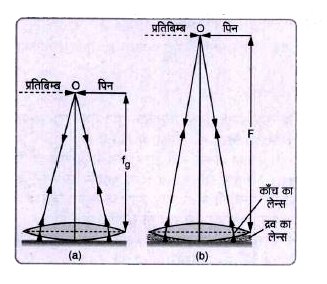
इससे स्पष्ट है कि पिन लेन्स के फोकस पर स्थित है।
अतः fg=+30 सेमी, (लेन्स उत्तल है)
दर्पण और लेन्स के बीच पारदर्शी द्रव डाल देने पर उनके बीच द्रव का एक समतल-अवतल (plano - concave) लेन्स बन जाता है अब पिन O को पूर्व स्थिति से ऊपर उठाने पर पिन O तथा उसके प्रतिबिम्ब में लम्बन नहीं रहता है।
पूर्व दशा की भाँति इस बार भी पिन काँच लेन्स तथा द्रव लेन्स के संयोजन से बने लेन्स के फोकस पर होगा।
अत: लेन्स संयोजन की फोकस दूरी fl है तो
1F=1fg+1fl
अथवा 1fl=1F−1fg
=150−130=−2150=−175
अथवा fl=−75 सेमी (अवतल)।
अतः f1=−75 द्रव के लेन्स का निचला पृष्ठ समतल है,
तथा R1=−20 सेमी (निर्देशांक ज्यामिति की चिह्न परिपाटी के अनुसार R ऋणात्मक होगा), अतः द्रव के लेन्स के लिए, 1fl=(n−1)(1R1−1∞)
=(n−1)R1=(n−1)(−20)
जहाँ n द्रव का वायु के सापेक्ष अपवर्तनांक है।
अत: n−1=−20fl=−20−75=415
अथवा n=1+415=1915=1.27.
Similar Questions
जब logk और 1/T के बीच एक आलेख आलेखित किया जाता है, तो हमें एक आलेख प्राप्त होता है, जैसा कि नीचे दर्शाया गया है आलेख में ढाल का मान क्या है?
View Solutionएक प्रवृत्ति, जो प्रथम वर्ग और 17वें वर्ग दोनों के तत्वों के लिए ऊपर से नीचे जाने पर एक समान होती है:
View SolutionNaCl के संकुलन प्रभाज के लिए निम्नलिखित में से कौन सा व्यंजक सही है, यदि एक फलक और एक विकर्ण से a- आयन को हटा दिया जाता है?
View Solutionकिसी धातु के टुकड़े के एक सिरे को गर्म करने पर दूसरा सिरा गर्म हो जाता है क्योंकि:
View Solutionजल के अणु के विलोपन के साथ ऐल्कोहॉल और एक अम्ल के बीच की अभिक्रिया को कहा जाता है
View Solutionदो द्रवों A और B के एक आदर्श मिश्रण को पिस्टन युक्त एक सिलेण्डर में रखा जाता है। पिस्टन को समतापीय रूप से खीचने पर द्रव का आयतन घटता है लेकिन वाष्प का आयतन बढ़ जाता है। द्रव की बहुत छोटी मात्रा शेष बचती है और वाष्प में A का मोल प्रभाज 0.4 होता है। यदि प्रायोगिक ताप पर P_(A)^(@)=0.4 और P_(B)^(@)=1.2" atm" है, तो निम्नलिखित में से किस कुल दाब पर द्रव लगभग वाष्पीकृत हो जाता है?
View Solutionयदि हाइड्रोजन और ऑक्सीजन को मिश्रित किया जाता है और कमरे के ताप पर, एक ही पात्र में रखा जाता है, तब जल के निर्माण के लिए अभिक्रिया नहीं होती है क्योकिं:
View Solutionद्रव 'A' के 100 mL को द्रव 'B' के 25 mL के साथ मिश्रित किया जाता है जिससे A-B मिश्रण का एक अनादर्श विलयन प्राप्त होता है जो राउल्ट के नियम से ऋणात्मक विचलन दर्शाता है। इस मिश्रण का आयतन होगा:
View Solution