एक समतलोत्तल लेन्स की मोटाई 4 सेमी है। जब इसे एक क्षैतिज मेज पर इस प्रकार रखा जाता है कि इसका वक्र पृष्ठ मेज के सम्पर्क में रहे तो लेन्स की तली के सबसे नीचे बिन्दु की गहराई 3 सेमी दिखाई देती है। यदि लेन्स को उलट दिया जाए जिससे समतल पृष्ठ मेज के सम्पर्क में रहे तो लेन्स के समतल पृष्ठ के केन्द्र की आभासी गहराई सेमी पायी जाती है। लेन्स की फोकस दूरी की गणना कीजिए।
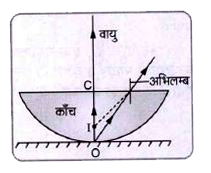
प्रथम स्थिति मे, लेन्स का वक्र पृष्ठ मेज के सम्पर्क में है। अत: यदि सम्पर्क बिन्दु O को बिन्दु वस्तु O माना जाए तो उससे चलने वाली प्रकाश किरणें लेन्स के समतलीय पृष्ठ से वायु में अपवर्तित होकर, बिन्दु वस्तु O का आभासी प्रतिबिम्ब I पर बनाएंगी।
समतल पृष्ठ पर अपवर्तन के लिए
सूत्र से
यहाँ सेमी, सेमी,
(समतल पृष्ठ)
चूंकि प्रकाश किरणें काँच से वायु में जा रही हैं, अत:
अथवा अत: काँच के सापेक्ष वायु का अपवर्तनांक
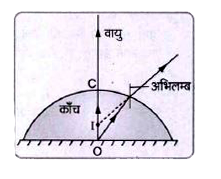
द्वितीय स्थिति में, लेन्स का समतल पृष्ठ मेज के सम्पर्क में है। यदि समतल पृष्ठ के केन्द्र O को बिन्दु वस्तु O माना जाए तो बिन्दु वस्तु O का आभासी प्रतिबिम्ब I बनेगा।
उत्तल पृष्ठ पर अपवर्तन के लिए
सूत्र से,
यहाँ सेमी
अथवा
अथवा ,
अतः सेमी
लेन्स की फोकस दूरी f के लिए -
दिया है सेमी,
लेन्स के सूत्र से
अत: लेन्स की फोकस दूरी f= 75 सेमी।
Similar Questions
एक शंकु की त्रिज्या 7 सेमी और ऊँचाई 9 सेमी है। इसका आयतन समान त्रिज्या वाले एक दूसरे शंकु के वक्र पृष्ठ के बराबर होता है। इस शंकु को तिर्यक ऊँचाई ज्ञात कीजिए।
View Solutionयदि वृत्त के केंद्र से 3 सेमी. की दूरी पर स्थित जीवा की लम्बाई 8 सेमी. है, तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionजब 'r त्रिज्या का एक हवा का बुलबुला किसी झील की तली से सतह तक उठता है तो उसकी त्रिज्या 5r/4 हो जाती है (वायुमण्डलीय दाब जल स्तम्भ की 10 मीटर की ऊंचाई के बराबर है)। यदि ताप नियत है तथा पृष्ठ तनाव को उपेक्षणीय माना गया है, तो झील की गहराई है
View Solutionएक पुस्तक की मोटाई 2 सेमी है और इसमें 800 पृष्ठ है। एक पृष्ठ की मोटाई मानक रूप में ज्ञात कीजिए।
View Solutionएक स्थिर आयतन ऊष्मातापी में अणुभार 28 की एक गैस के 3.5 gको 298.0K पर ऑक्सीजन के अधिवाकय में जलाया गया था दहन प्रक्रम के कारण उष्मामापी के टप्प 298.0K से 298.45 K तक की वृद्धि पायी गयी दिया हुआ है की उष्मामापी की उष्मा धारिता 2.5 kg K^-1 है गैस के दहन की अन्थेलपी का संख्यात्मक मान में है
View Solutionजब एक फ्लोराइड को काँच की नली में सांद्र H_(2)SO_(4) के साथ गर्म किया जाता है और यदि जल की एक बूंद को कांच की नली के मुख पर रखा जाता है, तो निम्नलिखित में से किसका श्वेत निक्षेप निर्मित होता है:
View Solutionसंगलित अशुद्ध धातु को लकड़ी के हरे रंग के लट्टे के साथ हिलाकर फफोलेदार तांबा को परिष्कृत किया जाता है, क्योंकि इस प्रकार की लकड़ी, हाइड्रोकार्बन गैसों (जैसे CH_4 ) को मुक्त करती है। इस प्रक्रम X को ________ कहा जाता है और इसका उपयोग धातु में प्रारंभ में उपस्थित Y की अशुद्धियों के शुद्धिकरण के लिए किया जाता है। Y _______ है।
View Solutionरेडियोएक्टिव ""^14C के क्षय के लिए अर्द्धआयु 5730 वर्ष है। लकड़ी की एक पुरातात्विक कलाकृति में ""^14C की सक्रियता, जीवित पेड़ों में पायी जाने वाली सक्रियता की 80% है। कलाकृति की आयु होगी: [दिया हुआ है: log 1.25 = 0.0969]
View Solution