Directions: Given data shows total male and female doctors in three hospital in a seminar. Read data carefully and answer the question:
In annual seminar of three hospitals, A, B and C some male and female doctors represent their hospitals. Average number of female doctors who represent A and B is 210. Total male doctors in A and B is 810. Number of female doctors is 23rd and 25th of male doctor in A and B repectively. Total female doctor who represent C are 25% more than total female doctor who represent A and total male doctor who represent C are 3313% more than female doctor who represent B.
Find the ratio between total male doctors who represent B and C together to total female doctors who represent A and C together?
23:13
23:14
23:18
23:12
The correct Answer is:C
To solve the problem step by step, let's break down the information given and derive the required values systematically.
Step 1: Define Variables
Let:
- MA = Number of male doctors in Hospital A
- MB = Number of male doctors in Hospital B
- FA = Number of female doctors in Hospital A
- FB = Number of female doctors in Hospital B
- FC = Number of female doctors in Hospital C
- MC = Number of male doctors in Hospital C
Step 2: Set Up Equations
From the problem statement, we have the following information:
1. Total male doctors in A and B:
MA+MB=810
2. Average number of female doctors in A and B:
FA+FB2=210⟹FA+FB=420
3. Female doctors in A are 23 of male doctors in A:
FA=23MA
4. Female doctors in B are 25 of male doctors in B:
FB=25MB
Step 3: Substitute and Solve for MA and MB
Substituting FA and FB into the equation FA+FB=420:
23MA+25MB=420
To eliminate the fractions, find a common denominator (which is 15):
10MA+6MB=6300(Multiplying through by 15)
Now we have two equations:
1. MA+MB=810
2. 10MA+6MB=6300
Step 4: Solve the System of Equations
From the first equation, express MA:
MA=810−MB
Substituting into the second equation:
10(810−MB)+6MB=6300
8100−10MB+6MB=6300
8100−4MB=6300
4MB=1800⟹MB=450
Now substitute back to find MA:
MA=810−450=360
Step 5: Calculate Female Doctors in A and B
Now calculate FA and FB:
FA=23×360=240
FB=25×450=180
Step 6: Calculate Female Doctors in C
Total female doctors in C are 25% more than total female doctors in A:
FC=FA+0.25FA=240+60=300
Step 7: Calculate Male Doctors in C
Total male doctors in C are 3313% more than female doctors in B:
MC=FB+13FB=180+60=240
Step 8: Calculate the Required Ratio
Now we need to find the ratio of total male doctors in B and C together to total female doctors in A and C together:
Total male doctors in B and C=MB+MC=450+240=690
Total female doctors in A and C=FA+FC=240+300=540
Step 9: Final Ratio
The required ratio is:
Ratio=690540=2318
Conclusion
Thus, the final answer is:
The ratio of total male doctors in B and C to total female doctors in A and C is 2318.
Let:
- MA = Number of male doctors in Hospital A
- MB = Number of male doctors in Hospital B
- FA = Number of female doctors in Hospital A
- FB = Number of female doctors in Hospital B
- FC = Number of female doctors in Hospital C
- MC = Number of male doctors in Hospital C
From the problem statement, we have the following information:
MA+MB=810
FA+FB2=210⟹FA+FB=420
FA=23MA
FB=25MB
Substituting FA and FB into the equation FA+FB=420:
23MA+25MB=420
10MA+6MB=6300(Multiplying through by 15)
1. MA+MB=810
2. 10MA+6MB=6300
From the first equation, express MA:
MA=810−MB
10(810−MB)+6MB=6300
8100−10MB+6MB=6300
8100−4MB=6300
4MB=1800⟹MB=450
MA=810−450=360
Now calculate FA and FB:
FA=23×360=240
FB=25×450=180
Total female doctors in C are 25% more than total female doctors in A:
FC=FA+0.25FA=240+60=300
Total male doctors in C are 3313% more than female doctors in B:
MC=FB+13FB=180+60=240
Now we need to find the ratio of total male doctors in B and C together to total female doctors in A and C together:
Total male doctors in B and C=MB+MC=450+240=690
Total female doctors in A and C=FA+FC=240+300=540
The required ratio is:
Ratio=690540=2318
Thus, the final answer is:
The ratio of total male doctors in B and C to total female doctors in A and C is 2318.
Similar Questions
Read the following information carefully and answer the questions given below.

Find the average difference between the number of male and female students in all the colleges?
View SolutionIn a family, there are 8 males and 4 females. The ratio of the number of females to the number of males is
View Solution
Knowledge Check
Number of females/ males in India
A933B930C927D940Doctor: Hospital
A(a) Farmer : VillageB(b) Chef : KitchenC(c) Plumber : WrenchD(d) Water : ReservoirDoctor : Hospital : : Chef : ?
AKnifeBKitchenCFoodDCook
Doctor : Hospital :: Teacher: _?_
View SolutionChoose the correct figure that represents the given relation:
Blue eyed, females, doctors
View SolutionThe following bar-diagram shows total number of males and females in five different organisations. Study it carefully to answer the questions.
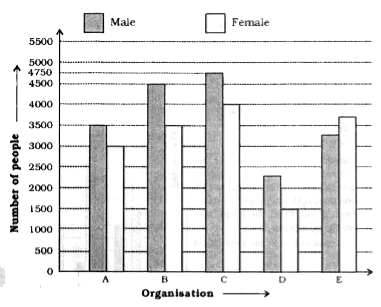
What is the ratio of average number of females from the organisations A, B and C to the average number of males from the organisations C, D and E?
View SolutionStudy the figure given below carefully and answer the questions that follow.
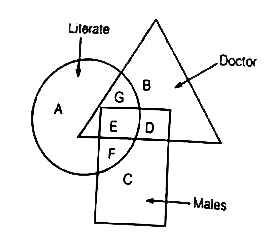
Which part shows Literate Males , who are Doctors ?
View SolutionStudy the figure given below carefully and answer the questions that follow.
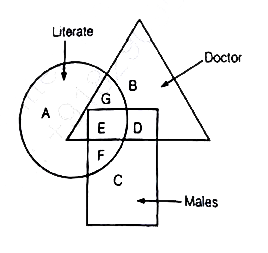
Which part shows Males who are neither Doctor nor Literate ?
View Solution
