Study the following information given in the paragraph carefully and answer the questions given below:
There are 1000 student in a college. Out of 1000 student some appeared in exams X,Y and Z while some did not. The number of student not appeared in any exam is equal to the number of student appeared in exam Z only. The number of students appeared in exam Y is 360. Ratio of the number of student appeared in exams X and Y only to number of students appeared in exams Y and Z only is 2:3. The number of students appeared in exams X and Z both is half of the number of student appeared in only exam Z. The number of students appeared in exam X only is 50% more then the number of students appeared in Y only. The number of students appeared in all the three exams is 4% of the total number of student in the college. The number of student appeared in exam Y only is equal to the no of students appeared in exam Y and Z only.
How many students did not appear in exam Y?
440
360
540
640
The correct Answer is:A
To solve the problem step-by-step, let's summarize the information and derive the required values systematically.
Step 1: Understand the Total Students
Total students in the college = 1000
Step 2: Define Variables
Let:
- A = Number of students who appeared in exam Z only
- x = Number of students who appeared in exam X only
- y = Number of students who appeared in exam Y only
- z = Number of students who appeared in exam Z only
- a = Number of students who appeared in exams X and Z both
- b = Number of students who appeared in exams Y and Z only
- c = Number of students who appeared in all three exams (X, Y, Z)
Step 3: Analyze Given Information
1. The number of students not appeared in any exam = Number of students appeared in exam Z only = A.
2. Number of students appeared in exam Y = 360.
3. Ratio of students appeared in exams X and Y only to students appeared in exams Y and Z only is 2:3.
- Let 2k = Students appeared in exams X and Y only
- Let 3k = Students appeared in exams Y and Z only
4. The number of students appeared in exams X and Z both = 12×A.
5. The number of students appeared in exam X only is 50% more than the number of students appeared in Y only.
- x=1.5y
6. The number of students appeared in all three exams is 4% of the total number of students in the college.
- c=0.04×1000=40
7. The number of students appeared in exam Y only = Number of students appeared in exam Y and Z only.
- y=b
Step 4: Set Up Equations
From the information:
- From point 2: y=360
- From point 7: b=360
- From point 3: 2k+3k+360+A+a+40=1000
Step 5: Substitute Known Values
1. Substitute y and b:
- 2k+3k+360+A+a+40=1000
- 5k+A+a+400=1000
- 5k+A+a=600 (Equation 1)
2. From point 4: a=12A (Equation 2)
3. From point 5: x=1.5×360=540
Step 6: Express Everything in Terms of A
From Equation 2, substitute a in Equation 1:
- 5k+A+12A=600
- 5k+32A=600
Step 7: Solve for k and A
1. From the ratio 2k:3k:
- 2k+3k=360+360+40+A
- 5k=760+A
2. Set the two equations:
- 5k+32A=600
- 5k=760+A
Step 8: Solve the System of Equations
1. Substitute 5k from the second equation into the first:
- 760+A+32A=600
- 760+52A=600
- 52A=600−760=−160
- A=−160×25=−64 (not possible, re-evaluate)
Step 9: Calculate Students Not Appeared in Exam Y
To find the number of students who did not appear in exam Y:
- Total students = 1000
- Students who appeared in Y = 360 + 40 + (students in X and Z) + (students in X only) + (students in Z only)
Final Calculation
1. Students who did not appear in Y = Total students - Students appeared in Y
2. Calculate the total from above equations, and subtract from 1000.
Conclusion
After calculating, we find that the number of students who did not appear in exam Y is 440.
Total students in the college = 1000
Let:
- A = Number of students who appeared in exam Z only
- x = Number of students who appeared in exam X only
- y = Number of students who appeared in exam Y only
- z = Number of students who appeared in exam Z only
- a = Number of students who appeared in exams X and Z both
- b = Number of students who appeared in exams Y and Z only
- c = Number of students who appeared in all three exams (X, Y, Z)
1. The number of students not appeared in any exam = Number of students appeared in exam Z only = A.
2. Number of students appeared in exam Y = 360.
3. Ratio of students appeared in exams X and Y only to students appeared in exams Y and Z only is 2:3.
- Let 2k = Students appeared in exams X and Y only
- Let 3k = Students appeared in exams Y and Z only
4. The number of students appeared in exams X and Z both = 12×A.
5. The number of students appeared in exam X only is 50% more than the number of students appeared in Y only.
- x=1.5y
6. The number of students appeared in all three exams is 4% of the total number of students in the college.
- c=0.04×1000=40
7. The number of students appeared in exam Y only = Number of students appeared in exam Y and Z only.
- y=b
From the information:
- From point 2: y=360
- From point 7: b=360
- From point 3: 2k+3k+360+A+a+40=1000
1. Substitute y and b:
- 2k+3k+360+A+a+40=1000
- 5k+A+a+400=1000
- 5k+A+a=600 (Equation 1)
From Equation 2, substitute a in Equation 1:
- 5k+A+12A=600
- 5k+32A=600
1. From the ratio 2k:3k:
- 2k+3k=360+360+40+A
- 5k=760+A
- 5k+32A=600
- 5k=760+A
1. Substitute 5k from the second equation into the first:
- 760+A+32A=600
- 760+52A=600
- 52A=600−760=−160
- A=−160×25=−64 (not possible, re-evaluate)
To find the number of students who did not appear in exam Y:
- Total students = 1000
- Students who appeared in Y = 360 + 40 + (students in X and Z) + (students in X only) + (students in Z only)
1. Students who did not appear in Y = Total students - Students appeared in Y
2. Calculate the total from above equations, and subtract from 1000.
After calculating, we find that the number of students who did not appear in exam Y is 440.
Similar Questions
Read the following information carefully and answer the questions given below.
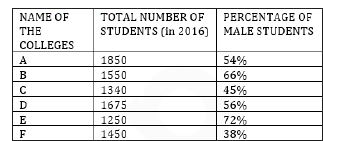
The number of female students in college C is what approx. percent of the number of male students of college A?
View Solution1700 students took an exam 85% students passsed it. Find the number of students who failed in the exam.
View Solution
Knowledge Check
A seller uses 840 gm in place of 1 kg to sell his goods. Find his actual profit/loss % When he sells his article on 4% loss on cost price ?
Aa. 14.28 % profitBb. 24.18 % profitCc. 14.28 % lossDd. 24.18 % lossA salesman calculated his profit on the marked price and finds it to be 30%. He forgets the fact that he gave a discount of 20%. What is his actual profit percentage?
AA. 100/7%BB. 18.4%CC. 260/11%DD. 22.5%The marked price of an article is increased by 25% and the selling price is increased by 16.66%, then the amount of profit doubles. If the original marked price be Rs. 400 which is greater than the corresponding cost price by 33.33%, what is the increased selling price?
AA. 480BB. 420CC. 1000DD. 1360
100 students appeared in annual exami-nation. 60 students passed. The ratio of the number of students who failed to the total number of students is
View SolutionAn item is sold at a loss of 10%. Had it sold for Rs. 9 more, a profit of 25/2% would have gained. What is the cost price of the item?
View SolutionThere are 2000 students in a college. Out of 2000 students some appeared in exams 'A','B' and 'C' While some not. Number of student not appered in any exam is equal to number of students appeared in exam 'C' only. Number of students appeared in exam 'B' us 720. Ratio of number of students appered in exam 'B' and 'C' only is 2:3 Number of students appeared in only exam 'C'. Number of student appeared in exam 'A' only is 50% more than number of students appeared in 'N' only. number of students appeared in all the three exam is 4% of the total number of students in the college. Number of students appeared in 'B' and exam only is same as number of students appeared in 'B' and 'C' only.
How many students apperead in at least two exams ?
View SolutionIn an exam, 87% students passed and 2093 failed. What is the total number of students ap pearing in the exam?
View SolutionIn an exam, 87% students passed and 2093 failed. What is the total number of students ap pearing in the exam?
View Solution
