Directions () : Study the following information carefully and answer the given questions
. Aman prints visiting cards of four standard sizes - (L×2) sq cm, (6×3) sq cm, (5×5) sq cm and (2×2) sq cm. On Monday he printed cards of two sizes (L×2) sq cm and (6×3) sq cm for a client. The respective ratio between the number of (L×2) sq cm cards and the number of (6×3) sq cm cards printed on Monday was 2:3. The client had to pay a total of rs 1600 for the (L×2) sq cm card and a total of rs 5400 for (6×3) sq cm card, (Both at the rate of 2rs per sq. cm).
What is the value of L?
3
8
5
4
The correct Answer is:D
To solve the problem, we need to find the value of L given the information about the visiting cards printed by Aman.
1. Understand the Sizes and Ratios:
- The sizes of the cards are:
- (L×2) sq cm
- (6×3) sq cm
- The ratio of the number of (L×2) sq cm cards to (6×3) sq cm cards printed is 2:3.
2. Assume Variables:
- Let the number of (L×2) cards printed be 2x.
- Let the number of (6×3) cards printed be 3x.
3. Calculate the Area of Each Card:
- Area of (L×2) card = 2L sq cm.
- Area of (6×3) card = 18 sq cm (since 6×3=18).
4. Calculate the Cost for Each Card:
- Cost of one (L×2) card = 2×(2L)=4L Rs.
- Cost of one (6×3) card = 2×18=36 Rs.
5. Total Cost for Each Type of Card:
- Total cost for (L×2) cards = 2x×4L=8xL.
- Total cost for (6×3) cards = 3x×36=108x.
6. Set Up the Equations:
- According to the problem, the total cost for (L×2) cards is Rs 1600:
8xL=1600
- The total cost for (6×3) cards is Rs 5400:
108x=5400
7. Solve for x:
- From 108x=5400:
x=5400108=50
8. Substitute x Back to Find L:
- Substitute x=50 into the equation 8xL=1600:
8×50×L=1600
400L=1600
L=1600400=4
Final Answer:
The value of L is 4.
- The sizes of the cards are:
- (L×2) sq cm
- (6×3) sq cm
- The ratio of the number of (L×2) sq cm cards to (6×3) sq cm cards printed is 2:3.
- Let the number of (L×2) cards printed be 2x.
- Let the number of (6×3) cards printed be 3x.
- Area of (L×2) card = 2L sq cm.
- Area of (6×3) card = 18 sq cm (since 6×3=18).
- Cost of one (L×2) card = 2×(2L)=4L Rs.
- Cost of one (6×3) card = 2×18=36 Rs.
- Total cost for (L×2) cards = 2x×4L=8xL.
- Total cost for (6×3) cards = 3x×36=108x.
- According to the problem, the total cost for (L×2) cards is Rs 1600:
8xL=1600
- The total cost for (6×3) cards is Rs 5400:
108x=5400
- From 108x=5400:
x=5400108=50
- Substitute x=50 into the equation 8xL=1600:
8×50×L=1600
400L=1600
L=1600400=4
The value of L is 4.
Similar Questions
The area of a side of a box is 120 sq. cm. The area of the other side of the box is 72 sq. cm. If the area of the upper surface of the box is 60 sq. cm. then find the volume of the box ?
View SolutionA block of steel of size 5cm×5cm×5 cm is weighed in water. If the relative density of steel is
View SolutionHow many small squares are there in 1sq.cm?
View SolutionHow many small squares are there in 1sq.cm?
View SolutionThe base area of a cuboid is 34 sq.cm . And height is 3.5 cm . What is the volume of cuboid ?
View SolutionThe area of the shaded portion is (FIGURE) (a) 10 sq. cm (b) 14 sq. cm (c) 21 sq. cm (d) 25 sq. cm
View SolutionAreas of two similar triangles are 225 sq cm and 81 sq cm. If a side of the smaller triangle is 12 cm, then find the corresponding side of the bigger triangle.
View SolutionThe perimeter of a sector is 24cm .Its maximum area in sq .cm is
View SolutionThe formula for the area, A sq cm of the white cross is
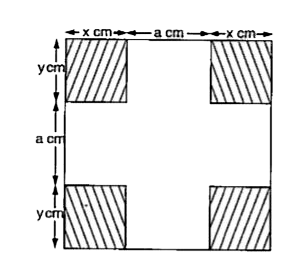
View SolutionWhat is the respective ratio between the length of a rectangle and side of a square?
I. Area of the square is 576 sq cm and the area of the rectangle is 600 sq cm
II. Breadth of the rectangle is half the side of the square.
View Solution
