Read the information given in the passage and answer the given question.
There are ‘X’ number of student in a college. Each of them likes either one or more of the following types of movies – Hollywood, Bollywood and Regional. The ratio of male to female student is 9:7. 16% of the male student like only Hollywood movies. 22% like only Bollywood movies . 12% like only Regional movies 30% of the male students like only Hollywood and Bollywood movies. 10% like only Bollywood and Regional movies and 6% like only Regional and Hollywood movies. The remaining 18 male students like all the given type of movies.
14% of the female students like only Hollywood movies. 20% like only Bollywood movies. 8% like only Regional movies. 26% of the female students like only Hollywood and Bollywood movies. 18% like only Bollywood and Regional movies and 10% like only Regional and Hollywood movies. The remaining female students like all the given type of movies.
The number of male students who like only two of the given types of movies is what per cent more than the number of female student who like only two of the given types of movies?
11121
1617
91121
817
The correct Answer is:C
To solve the problem step-by-step, we will first summarize the information provided and then calculate the required values.
Step 1: Define the Variables
Let the total number of male students be M and female students be F. According to the problem, the ratio of male to female students is 9:7. We can express this as:
- M=9x
- F=7x
Step 2: Calculate Male Students
From the problem, we know:
- 16% of male students like only Hollywood movies: 0.16M=0.16(9x)=1.44x
- 22% like only Bollywood movies: 0.22M=0.22(9x)=1.98x
- 12% like only Regional movies: 0.12M=0.12(9x)=1.08x
- 30% like only Hollywood and Bollywood: 0.30M=0.30(9x)=2.7x
- 10% like only Bollywood and Regional: 0.10M=0.10(9x)=0.9x
- 6% like only Regional and Hollywood: 0.06M=0.06(9x)=0.54x
- Remaining male students like all three types of movies: 18
Step 3: Calculate Total Percentage for Males
Now, we will sum the percentages of male students who like one or two types of movies:
16+22+12+30+10+6=96%
This means 4% of male students like all three types of movies. Thus, we can set up the equation:
0.04M=18⟹M=180.04=450
So, M=450 and substituting back, we find x:
9x=450⟹x=50
Thus, F=7x=350.
Step 4: Calculate Female Students
Now we will calculate the number of female students who like different types of movies:
- 14% like only Hollywood: 0.14F=0.14(350)=49
- 20% like only Bollywood: 0.20F=0.20(350)=70
- 8% like only Regional: 0.08F=0.08(350)=28
- 26% like only Hollywood and Bollywood: 0.26F=0.26(350)=91
- 18% like only Bollywood and Regional: 0.18F=0.18(350)=63
- 10% like only Regional and Hollywood: 0.10F=0.10(350)=35
- Remaining female students like all three types of movies.
Step 5: Calculate Total Percentage for Females
Now, we will sum the percentages of female students who like one or two types of movies:
14+20+8+26+18+10=96%
This means 4% of female students like all three types of movies:
0.04F=0.04(350)=14
Step 6: Calculate Male and Female Students Who Like Only Two Types of Movies
For males:
- Only Hollywood and Bollywood: 2.7x=2.7(50)=135
- Only Bollywood and Regional: 0.9x=0.9(50)=45
- Only Regional and Hollywood: 0.54x=0.54(50)=27
Total males who like only two types of movies:
135+45+27=207
For females:
- Only Hollywood and Bollywood: 91
- Only Bollywood and Regional: 63
- Only Regional and Hollywood: 35
Total females who like only two types of movies:
91+63+35=189
Step 7: Calculate the Percentage Difference
Now we need to find out what percentage more the number of male students who like only two types of movies is compared to female students who like only two types of movies:
Difference=207−189=18
Percentage more=(18189)×100≈9.52%
Final Answer
The number of male students who like only two of the given types of movies is approximately 9.52% more than the number of female students who like only two of the given types of movies.
Let the total number of male students be M and female students be F. According to the problem, the ratio of male to female students is 9:7. We can express this as:
- M=9x
- F=7x
From the problem, we know:
- 16% of male students like only Hollywood movies: 0.16M=0.16(9x)=1.44x
- 22% like only Bollywood movies: 0.22M=0.22(9x)=1.98x
- 12% like only Regional movies: 0.12M=0.12(9x)=1.08x
- 30% like only Hollywood and Bollywood: 0.30M=0.30(9x)=2.7x
- 10% like only Bollywood and Regional: 0.10M=0.10(9x)=0.9x
- 6% like only Regional and Hollywood: 0.06M=0.06(9x)=0.54x
- Remaining male students like all three types of movies: 18
Now, we will sum the percentages of male students who like one or two types of movies:
16+22+12+30+10+6=96%
This means 4% of male students like all three types of movies. Thus, we can set up the equation:
0.04M=18⟹M=180.04=450
So, M=450 and substituting back, we find x:
9x=450⟹x=50
Thus, F=7x=350.
Now we will calculate the number of female students who like different types of movies:
- 14% like only Hollywood: 0.14F=0.14(350)=49
- 20% like only Bollywood: 0.20F=0.20(350)=70
- 8% like only Regional: 0.08F=0.08(350)=28
- 26% like only Hollywood and Bollywood: 0.26F=0.26(350)=91
- 18% like only Bollywood and Regional: 0.18F=0.18(350)=63
- 10% like only Regional and Hollywood: 0.10F=0.10(350)=35
- Remaining female students like all three types of movies.
Now, we will sum the percentages of female students who like one or two types of movies:
14+20+8+26+18+10=96%
This means 4% of female students like all three types of movies:
0.04F=0.04(350)=14
For males:
- Only Hollywood and Bollywood: 2.7x=2.7(50)=135
- Only Bollywood and Regional: 0.9x=0.9(50)=45
- Only Regional and Hollywood: 0.54x=0.54(50)=27
135+45+27=207
- Only Hollywood and Bollywood: 91
- Only Bollywood and Regional: 63
- Only Regional and Hollywood: 35
91+63+35=189
Now we need to find out what percentage more the number of male students who like only two types of movies is compared to female students who like only two types of movies:
Difference=207−189=18
Percentage more=(18189)×100≈9.52%
The number of male students who like only two of the given types of movies is approximately 9.52% more than the number of female students who like only two of the given types of movies.
Similar Questions
In a class, each student likes either cricket or football, 40% of the students like football, 80% of the students like cricket. The number of students who like only cricket is 40 more than the number of students who like only football. Then the strength of the class is :
View Solution44% of the students in a class are females and the number of male students is 42. Find the total no. of students in the class.
View Solution
Knowledge Check
In a class, each student likes either cricket or football 40% of the students like football. 80% of the students like cricket. The number of studnets who like only cricket is 40 more than the number of students who like only football. What is the strength of the class?
A80B100C120D150In a school 80 students like chocolate, 40 like coffee if the number of students doesn't like any of them is equal to the number of students who like both of them then what is the total number of students in the school?
A115B90C120DNone of theseThe sum of the number of male and female students in an institute is 100. If the number of male students is x, then the number of female students becomes x % of the total number of students. Find the number of male students.
A(A) 60B(B) 65C(C) 50D(D) 45
Read the following information carefully and answer the questions given below.
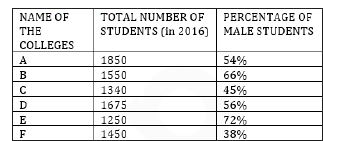
The number of female students in college C is what approx. percent of the number of male students of college A?
View SolutionIn a class of 50 students 32 likes Mathematics , 24 like Science and 12 like both . Find the number of students who like neither of the two subjects.
View SolutionRead the following information carefully and answer the questions given below.

Find the average difference between the number of male and female students in all the colleges?
View SolutionThe pie chart given below shows the distribution of students who like the given 5 sports. The total number of students is 960.
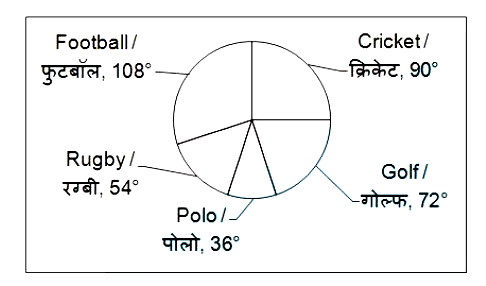
What is the difference between the number of students who like Cricket and those who like Golf?
View SolutionA survey of students was made to know which games they like. The number of students who liked football was presented in the pie diagram by the central angle 63∘. What is the percentage of these students of the total number of student ?
View Solution
